3 Comparison of two PCA packages
Datasets:
decathlon2-
Algorithms:
- PCA
3.2 General methods for principal component analysis
There are two general methods to perform PCA in R :
- Spectral decomposition which examines the covariances / correlations between variables
- Singular value decomposition which examines the covariances / correlations between individuals
The function princomp() uses the spectral decomposition approach. The functions prcomp() and PCA()[FactoMineR] use the singular value decomposition (SVD).
3.2.1 prcomp() and princomp() functions
The simplified format of these 2 functions are :
prcomp(x, scale = FALSE)
princomp(x, cor = FALSE, scores = TRUE)Arguments for prcomp():
x: a numeric matrix or data framescale: a logical value indicating whether the variables should be scaled to have unit variance before the analysis takes placeArguments for princomp():
x: a numeric matrix or data framecor: a logical value. If TRUE, the data will be centered and scaled before the analysisscores: a logical value. If TRUE, the coordinates on each principal component are calculated
3.2.2 Loading factoextra
# install.packages("factoextra")
library(factoextra)
#> Loading required package: ggplot2
#> Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa3.2.3 Loading the decathlon dataset
We’ll use the data sets decathlon2 [in factoextra], which has been already described at: PCA - Data format.
Briefly, it contains:
- Active individuals (rows 1 to 23) and active variables (columns 1 to 10), which are used to perform the principal component analysis
- Supplementary individuals (rows 24 to 27) and supplementary variables (columns 11 to 13), which coordinates will be predicted using the PCA information and parameters obtained with active individuals/variables.
library("factoextra")
data(decathlon2)
decathlon2.active <- decathlon2[1:23, 1:10]
head(decathlon2.active[, 1:6])
#> X100m Long.jump Shot.put High.jump X400m X110m.hurdle
#> SEBRLE 11.0 7.58 14.8 2.07 49.8 14.7
#> CLAY 10.8 7.40 14.3 1.86 49.4 14.1
#> BERNARD 11.0 7.23 14.2 1.92 48.9 15.0
#> YURKOV 11.3 7.09 15.2 2.10 50.4 15.3
#> ZSIVOCZKY 11.1 7.30 13.5 2.01 48.6 14.2
#> McMULLEN 10.8 7.31 13.8 2.13 49.9 14.4
decathlon2.supplementary <- decathlon2[24:27, 1:10]
head(decathlon2.supplementary[, 1:6])
#> X100m Long.jump Shot.put High.jump X400m X110m.hurdle
#> KARPOV 11.0 7.30 14.8 2.04 48.4 14.1
#> WARNERS 11.1 7.60 14.3 1.98 48.7 14.2
#> Nool 10.8 7.53 14.3 1.88 48.8 14.8
#> Drews 10.9 7.38 13.1 1.88 48.5 14.03.3 Compute PCA in R using prcomp()
In this section we’ll provide an easy-to-use R code to compute and visualize PCA in R using the prcomp() function and the factoextra package.
`. Load factoextra for visualization
- compute PCA
# compute PCA
res.pca <- prcomp(decathlon2.active, scale = TRUE)- Visualize eigenvalues (scree plot). Show the percentage of variances explained by each principal component.
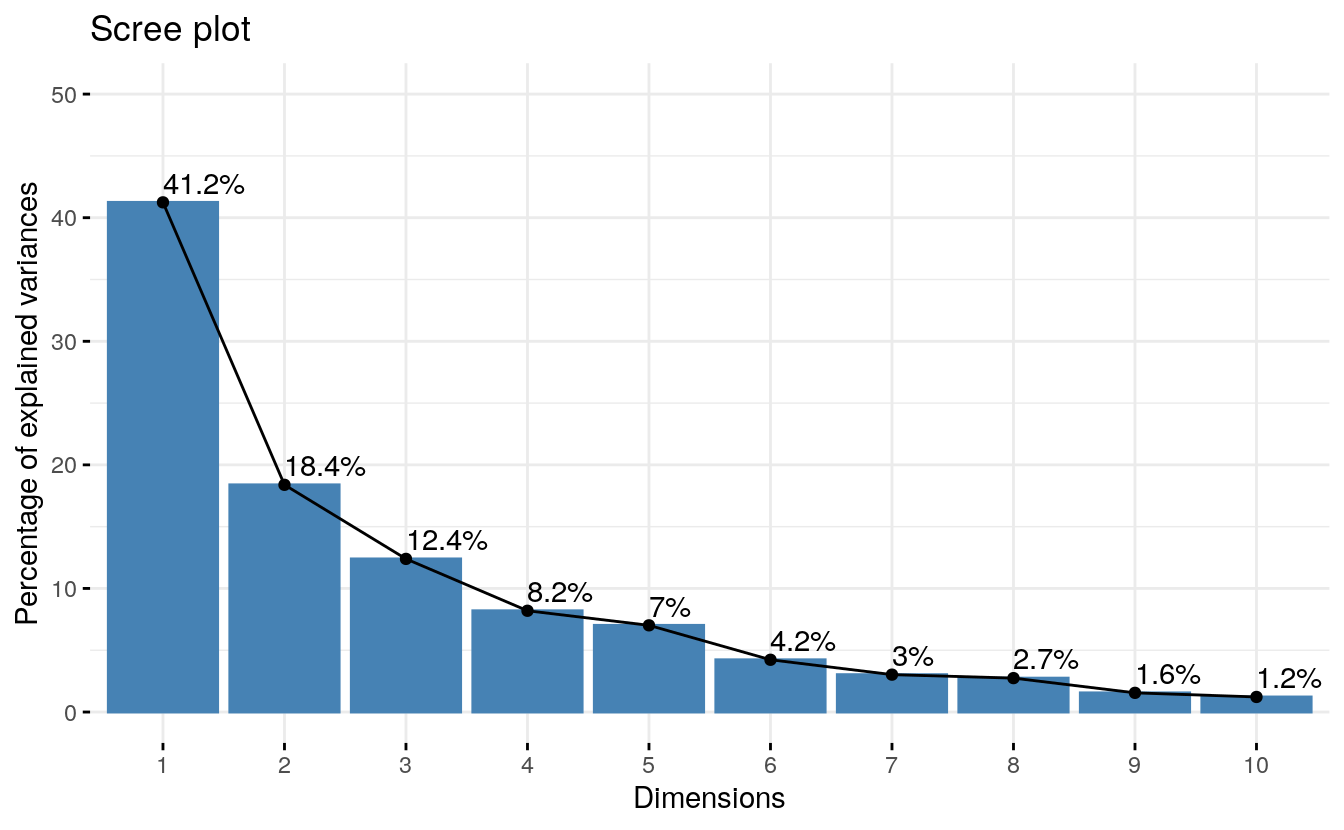
From the plot above, we might want to stop at the fifth principal component. 87% of the information (variances) contained in the data are retained by the first five principal components.
3.4 Plots: quality and contribution
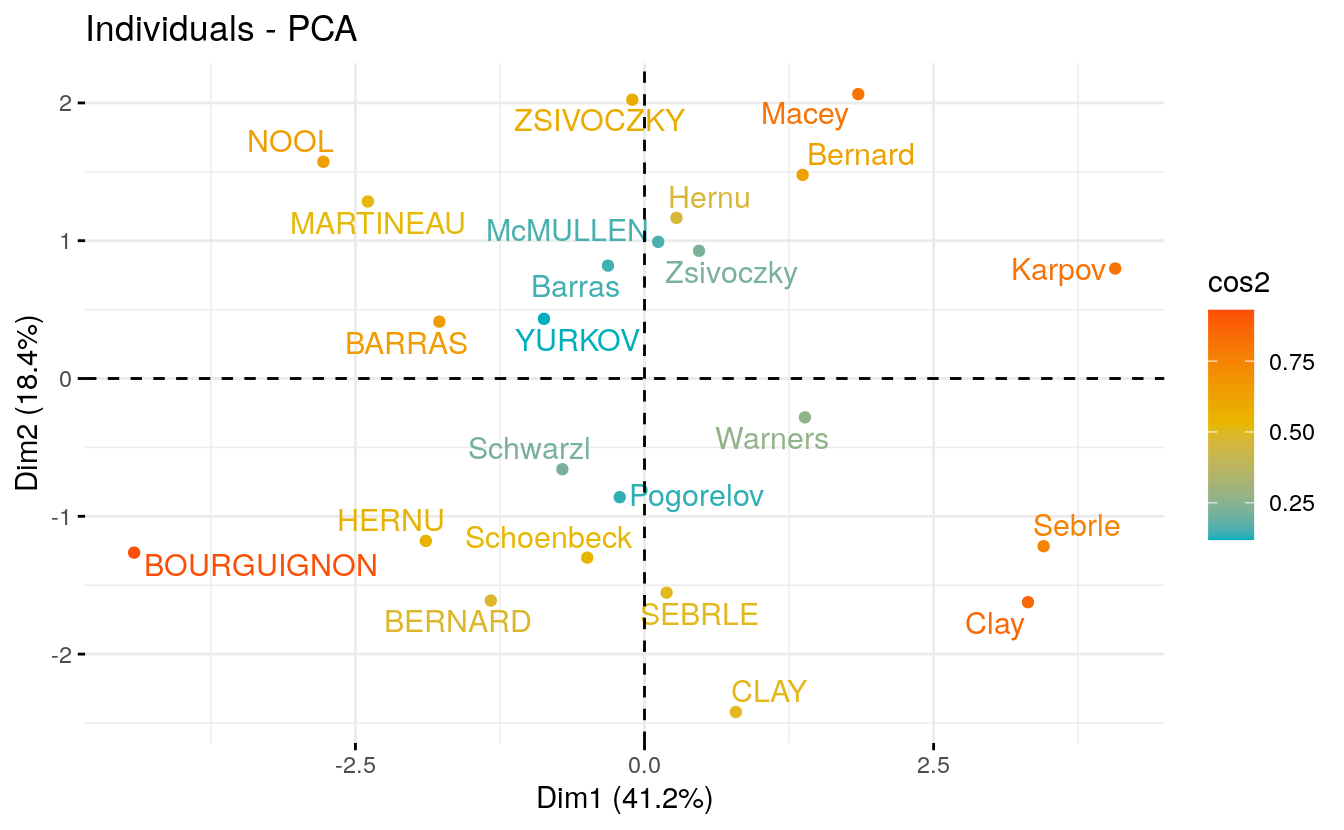
- Graph of individuals. Individuals with a similar profile are grouped together.
# Graph of individuals.
fviz_pca_ind(res.pca,
col.ind = "cos2", # Color by the quality of representation
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE # Avoid text overlapping
)
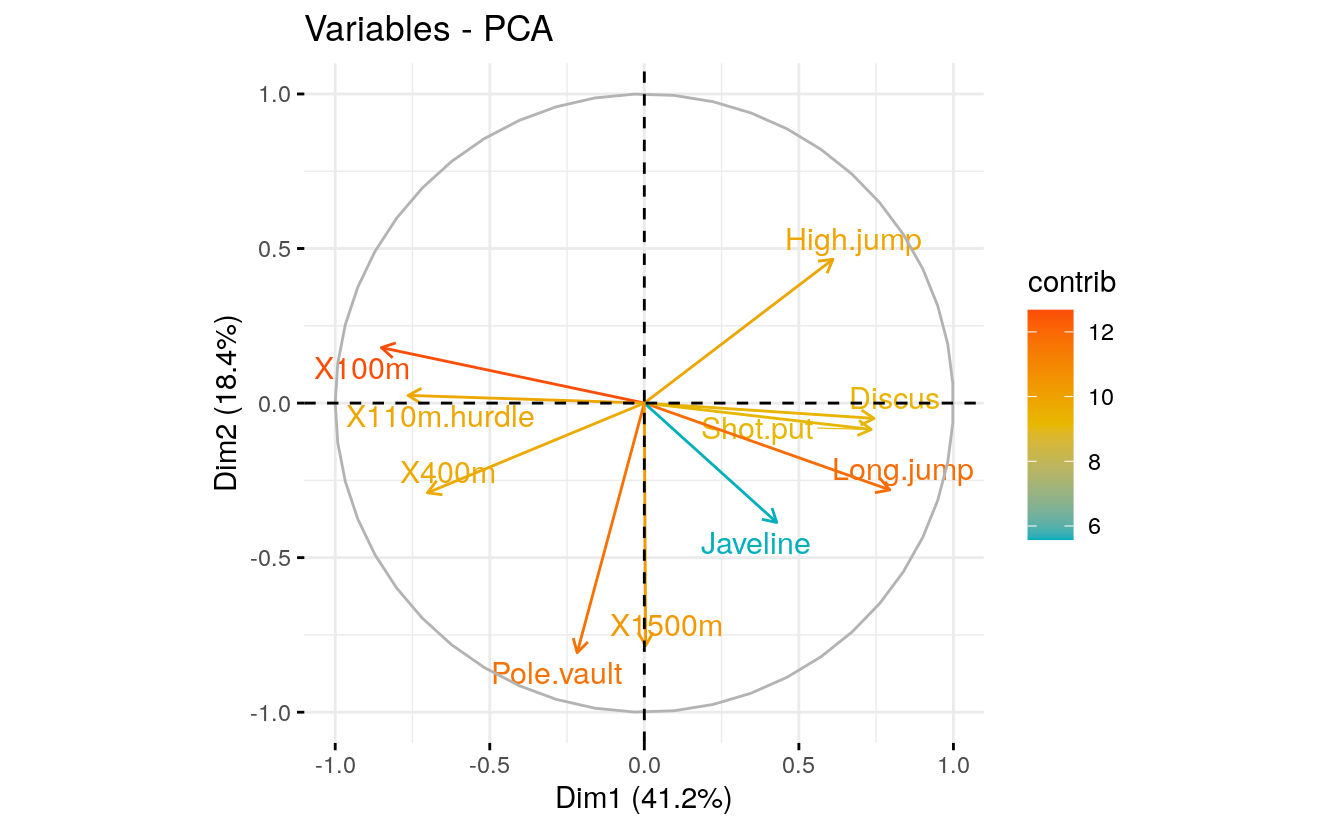
- Graph of variables. Positive correlated variables point to the same side of the plot. Negative correlated variables point to opposite sides of the graph.
# Graph of variables.
fviz_pca_var(res.pca,
col.var = "contrib", # Color by contributions to the PC
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE # Avoid text overlapping
)
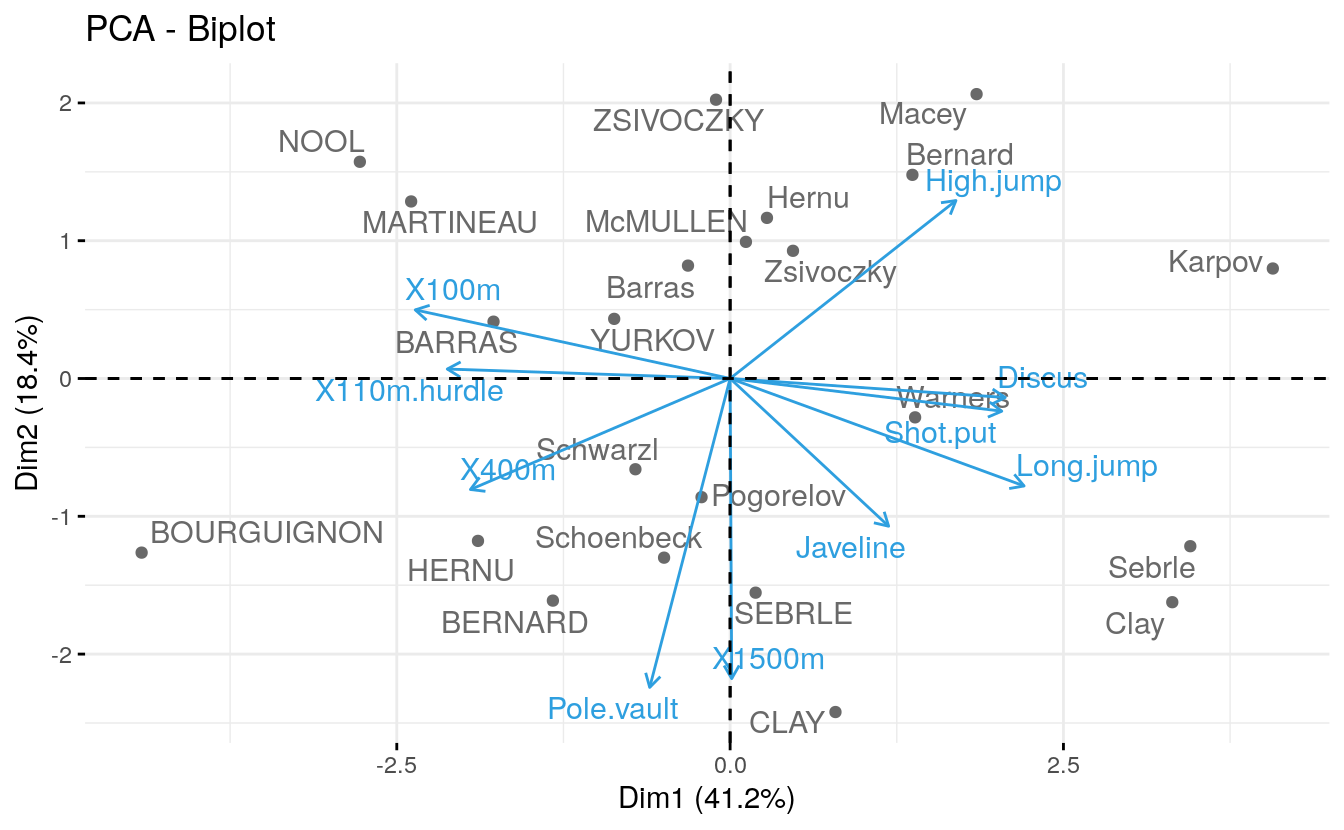
- Biplot of individuals and variables
# Biplot of individuals and variables
fviz_pca_biplot(res.pca, repel = TRUE,
col.var = "#2E9FDF", # Variables color
col.ind = "#696969" # Individuals color
)
3.5 Access to the PCA results
library(factoextra)
# Eigenvalues
eig.val <- get_eigenvalue(res.pca)
eig.val
#> eigenvalue variance.percent cumulative.variance.percent
#> Dim.1 4.124 41.24 41.2
#> Dim.2 1.839 18.39 59.6
#> Dim.3 1.239 12.39 72.0
#> Dim.4 0.819 8.19 80.2
#> Dim.5 0.702 7.02 87.2
#> Dim.6 0.423 4.23 91.5
#> Dim.7 0.303 3.03 94.5
#> Dim.8 0.274 2.74 97.2
#> Dim.9 0.155 1.55 98.8
#> Dim.10 0.122 1.22 100.0
# Results for Variables
res.var <- get_pca_var(res.pca)
res.var$coord # Coordinates
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8
#> X100m -0.85063 0.1794 -0.3016 0.0336 -0.194 0.03537 -0.09134 -0.10472
#> Long.jump 0.79418 -0.2809 0.1905 -0.1154 0.233 -0.03373 -0.15433 -0.39738
#> Shot.put 0.73391 -0.0854 -0.5176 0.1285 -0.249 -0.23979 -0.00989 0.02436
#> High.jump 0.61008 0.4652 -0.3301 0.1446 0.403 -0.28464 0.02816 0.08441
#> X400m -0.70160 -0.2902 -0.2835 0.4308 0.104 -0.04929 0.28611 -0.23355
#> X110m.hurdle -0.76413 0.0247 -0.4489 -0.0169 0.224 0.00263 -0.37007 -0.00834
#> Discus 0.74321 -0.0497 -0.1765 0.3950 -0.408 0.19854 -0.14273 -0.03956
#> Pole.vault -0.21727 -0.8075 -0.0941 -0.3390 -0.222 -0.32746 -0.01039 0.03291
#> Javeline 0.42823 -0.3861 -0.6041 -0.3317 0.198 0.36210 0.13356 0.05284
#> X1500m 0.00428 -0.7845 0.2195 0.4480 0.263 0.04205 -0.11137 0.19447
#> Dim.9 Dim.10
#> X100m -0.3031 0.04442
#> Long.jump -0.0516 0.02972
#> Shot.put 0.0478 0.21745
#> High.jump -0.1121 -0.13357
#> X400m 0.0822 -0.03417
#> X110m.hurdle 0.1618 -0.01563
#> Discus 0.0134 -0.17259
#> Pole.vault -0.0258 -0.13721
#> Javeline -0.0405 -0.00385
#> X1500m -0.1022 0.06283
res.var$contrib # Contributions to the PCs
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8
#> X100m 1.75e+01 1.7505 7.339 0.1376 5.39 0.29592 2.7571 3.9952
#> Long.jump 1.53e+01 4.2904 2.930 1.6249 7.75 0.26900 7.8716 57.5332
#> Shot.put 1.31e+01 0.3967 21.620 2.0141 8.82 13.59686 0.0323 0.2162
#> High.jump 9.02e+00 11.7716 8.793 2.5499 23.12 19.15961 0.2620 2.5957
#> X400m 1.19e+01 4.5799 6.488 22.6509 1.54 0.57451 27.0527 19.8734
#> X110m.hurdle 1.42e+01 0.0333 16.261 0.0348 7.17 0.00164 45.2616 0.0254
#> Discus 1.34e+01 0.1341 2.515 19.0413 23.76 9.32175 6.7323 0.5702
#> Pole.vault 1.14e+00 35.4619 0.714 14.0231 7.01 25.35762 0.0357 0.3947
#> Javeline 4.45e+00 8.1087 29.453 13.4296 5.58 31.00496 5.8957 1.0173
#> X1500m 4.44e-04 33.4729 3.887 24.4939 9.88 0.41813 4.0989 13.7787
#> Dim.9 Dim.10
#> X100m 59.174 1.6176
#> Long.jump 1.715 0.7241
#> Shot.put 1.471 38.7677
#> High.jump 8.102 14.6265
#> X400m 4.349 0.9573
#> X110m.hurdle 16.858 0.2003
#> Discus 0.115 24.4217
#> Pole.vault 0.428 15.4356
#> Javeline 1.054 0.0122
#> X1500m 6.734 3.2370
res.var$cos2 # Quality of representation
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7
#> X100m 7.24e-01 0.032184 0.09094 0.001127 0.0378 1.25e-03 8.34e-03
#> Long.jump 6.31e-01 0.078881 0.03631 0.013315 0.0544 1.14e-03 2.38e-02
#> Shot.put 5.39e-01 0.007294 0.26791 0.016504 0.0619 5.75e-02 9.77e-05
#> High.jump 3.72e-01 0.216424 0.10896 0.020895 0.1622 8.10e-02 7.93e-04
#> X400m 4.92e-01 0.084203 0.08039 0.185611 0.0108 2.43e-03 8.19e-02
#> X110m.hurdle 5.84e-01 0.000612 0.20150 0.000285 0.0503 6.93e-06 1.37e-01
#> Discus 5.52e-01 0.002466 0.03116 0.156032 0.1667 3.94e-02 2.04e-02
#> Pole.vault 4.72e-02 0.651977 0.00885 0.114911 0.0491 1.07e-01 1.08e-04
#> Javeline 1.83e-01 0.149080 0.36497 0.110048 0.0391 1.31e-01 1.78e-02
#> X1500m 1.83e-05 0.615409 0.04817 0.200713 0.0693 1.77e-03 1.24e-02
#> Dim.8 Dim.9 Dim.10
#> X100m 1.10e-02 0.091848 1.97e-03
#> Long.jump 1.58e-01 0.002661 8.83e-04
#> Shot.put 5.93e-04 0.002284 4.73e-02
#> High.jump 7.12e-03 0.012575 1.78e-02
#> X400m 5.45e-02 0.006750 1.17e-03
#> X110m.hurdle 6.96e-05 0.026166 2.44e-04
#> Discus 1.56e-03 0.000179 2.98e-02
#> Pole.vault 1.08e-03 0.000664 1.88e-02
#> Javeline 2.79e-03 0.001637 1.49e-05
#> X1500m 3.78e-02 0.010453 3.95e-03
# Results for individuals
res.ind <- get_pca_ind(res.pca)
res.ind$coord # Coordinates
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8
#> SEBRLE 0.191 -1.554 -0.628 0.0821 1.142614 -0.4639 -0.2080 0.04346
#> CLAY 0.790 -2.420 1.357 1.2698 -0.806848 1.3042 -0.2129 0.61724
#> BERNARD -1.329 -1.612 -0.196 -1.9209 0.082343 -0.4006 -0.4064 0.70386
#> YURKOV -0.869 0.433 -2.474 0.6972 0.398858 0.1029 -0.3249 0.11500
#> ZSIVOCZKY -0.106 2.023 1.305 -0.0993 -0.197024 0.8955 0.0883 -0.20234
#> McMULLEN 0.119 0.992 0.844 1.3122 1.585871 0.1866 0.4783 0.29309
#> MARTINEAU -2.392 1.285 -0.898 0.3731 -2.243352 -0.4567 -0.2998 -0.29163
#> HERNU -1.891 -1.178 -0.156 0.8913 -0.126741 0.4362 -0.5661 -1.52940
#> BARRAS -1.774 0.413 0.658 0.2287 -0.233837 0.0903 0.2159 0.68258
#> NOOL -2.777 1.573 0.607 -1.5555 1.424184 0.4972 -0.5321 -0.43339
#> BOURGUIGNON -4.414 -1.264 -0.010 0.6668 0.419152 -0.0820 -0.5983 0.56362
#> Sebrle 3.451 -1.217 -1.678 -0.8087 -0.025053 -0.0828 0.0102 -0.03059
#> Clay 3.316 -1.623 -0.618 -0.3168 0.569165 0.7772 0.2575 -0.58064
#> Karpov 4.070 0.798 1.015 0.3134 -0.797426 -0.3296 -1.3637 0.34531
#> Macey 1.848 2.064 -0.979 0.5847 -0.000216 -0.1973 -0.2693 -0.36322
#> Warners 1.387 -0.282 2.000 -1.0196 -0.040540 -0.5567 -0.2674 -0.10947
#> Zsivoczky 0.472 0.927 -1.728 -0.1848 0.407303 -0.1138 0.0399 0.53804
#> Hernu 0.276 1.166 0.171 -0.8487 -0.689480 -0.3317 0.4431 0.24729
#> Bernard 1.367 1.478 0.831 0.7453 0.859802 -0.3281 0.3636 0.00617
#> Schwarzl -0.710 -0.658 1.041 -0.9272 -0.288757 -0.6889 0.5657 -0.68705
#> Pogorelov -0.214 -0.861 0.298 1.3556 -0.015053 -1.5938 0.7837 -0.03762
#> Schoenbeck -0.495 -1.300 0.103 -0.2493 -0.645226 0.1617 0.8575 -0.25585
#> Barras -0.316 0.819 -0.862 -0.5894 -0.779739 1.1742 0.9451 0.36555
#> Dim.9 Dim.10
#> SEBRLE -0.65934 0.0327
#> CLAY -0.06013 -0.3172
#> BERNARD 0.17008 -0.0991
#> YURKOV -0.10952 -0.1197
#> ZSIVOCZKY -0.52310 -0.3484
#> McMULLEN -0.10562 -0.3932
#> MARTINEAU -0.22342 -0.6164
#> HERNU 0.00618 0.5537
#> BARRAS -0.66928 0.5309
#> NOOL -0.11578 -0.0962
#> BOURGUIGNON 0.52581 0.0586
#> Sebrle -0.84721 0.2197
#> Clay 0.40978 -0.6160
#> Karpov 0.19306 0.2172
#> Macey 0.36826 0.2125
#> Warners 0.18028 0.2421
#> Zsivoczky 0.58597 -0.1427
#> Hernu 0.06691 -0.2087
#> Bernard 0.27949 0.3207
#> Schwarzl -0.00836 -0.3021
#> Pogorelov -0.13053 -0.0370
#> Schoenbeck 0.56422 0.2968
#> Barras 0.10226 0.6119
res.ind$contrib # Contributions to the PCs
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8
#> SEBRLE 0.0385 5.712 1.39e+00 0.0357 8.09e+00 2.2126 0.62143 2.99e-02
#> CLAY 0.6581 13.854 6.46e+00 8.5557 4.03e+00 17.4880 0.65141 6.04e+00
#> BERNARD 1.8627 6.144 1.35e-01 19.5783 4.20e-02 1.6502 2.37365 7.85e+00
#> YURKOV 0.7969 0.443 2.15e+01 2.5794 9.86e-01 0.1088 1.51656 2.09e-01
#> ZSIVOCZKY 0.0118 9.682 5.97e+00 0.0523 2.41e-01 8.2456 0.11192 6.49e-01
#> McMULLEN 0.0148 2.325 2.50e+00 9.1353 1.56e+01 0.3579 3.28702 1.36e+00
#> MARTINEAU 6.0337 3.904 2.83e+00 0.7386 3.12e+01 2.1441 1.29111 1.35e+00
#> HERNU 3.7700 3.284 8.58e-02 4.2151 9.96e-02 1.9566 4.60485 3.71e+01
#> BARRAS 3.3194 0.402 1.52e+00 0.2776 3.39e-01 0.0838 0.67004 7.38e+00
#> NOOL 8.1299 5.849 1.29e+00 12.8376 1.26e+01 2.5413 4.06767 2.98e+00
#> BOURGUIGNON 20.5373 3.776 3.53e-04 2.3588 1.09e+00 0.0691 5.14425 5.03e+00
#> Sebrle 12.5584 3.502 9.88e+00 3.4701 3.89e-03 0.0705 0.00148 1.48e-02
#> Clay 11.5936 6.232 1.34e+00 0.5325 2.01e+00 6.2097 0.95282 5.34e+00
#> Karpov 17.4661 1.507 3.61e+00 0.5210 3.94e+00 1.1168 26.72016 1.89e+00
#> Macey 3.6021 10.073 3.36e+00 1.8139 2.89e-07 0.4001 1.04191 2.09e+00
#> Warners 2.0291 0.188 1.40e+01 5.5159 1.02e-02 3.1867 1.02738 1.90e-01
#> Zsivoczky 0.2344 2.031 1.05e+01 0.1813 1.03e+00 0.1332 0.02289 4.59e+00
#> Hernu 0.0805 3.214 1.02e-01 3.8217 2.95e+00 1.1311 2.82103 9.69e-01
#> Bernard 1.9708 5.166 2.43e+00 2.9474 4.58e+00 1.1066 1.89945 6.02e-04
#> Schwarzl 0.5318 1.025 3.80e+00 4.5612 5.17e-01 4.8796 4.59812 7.48e+00
#> Pogorelov 0.0484 1.753 3.11e-01 9.7503 1.40e-03 26.1167 8.82532 2.24e-02
#> Schoenbeck 0.2586 3.997 3.72e-02 0.3297 2.58e+00 0.2689 10.56627 1.04e+00
#> Barras 0.1052 1.588 2.61e+00 1.8430 3.77e+00 14.1743 12.83542 2.12e+00
#> Dim.9 Dim.10
#> SEBRLE 12.17748 0.0382
#> CLAY 0.10126 3.5857
#> BERNARD 0.81032 0.3499
#> YURKOV 0.33601 0.5107
#> ZSIVOCZKY 7.66492 4.3274
#> McMULLEN 0.31250 5.5105
#> MARTINEAU 1.39820 13.5440
#> HERNU 0.00107 10.9278
#> BARRAS 12.54733 10.0454
#> NOOL 0.37548 0.3300
#> BOURGUIGNON 7.74457 0.1222
#> Sebrle 20.10555 1.7206
#> Clay 4.70357 13.5271
#> Karpov 1.04399 1.6819
#> Macey 3.79877 1.6096
#> Warners 0.91042 2.0890
#> Zsivoczky 9.61785 0.7261
#> Hernu 0.12540 1.5523
#> Bernard 2.18807 3.6657
#> Schwarzl 0.00196 3.2536
#> Pogorelov 0.47727 0.0487
#> Schoenbeck 8.91730 3.1402
#> Barras 0.29289 13.3453
res.ind$cos2 # Quality of representation
#> Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8
#> SEBRLE 0.00753 0.4975 8.13e-02 0.00139 2.69e-01 0.044324 8.91e-03 3.89e-04
#> CLAY 0.04870 0.4570 1.44e-01 0.12579 5.08e-02 0.132691 3.54e-03 2.97e-02
#> BERNARD 0.19720 0.2900 4.29e-03 0.41182 7.57e-04 0.017913 1.84e-02 5.53e-02
#> YURKOV 0.09611 0.0238 7.78e-01 0.06181 2.02e-02 0.001345 1.34e-02 1.68e-03
#> ZSIVOCZKY 0.00157 0.5764 2.40e-01 0.00139 5.47e-03 0.112918 1.10e-03 5.76e-03
#> McMULLEN 0.00218 0.1522 1.10e-01 0.26649 3.89e-01 0.005388 3.54e-02 1.33e-02
#> MARTINEAU 0.40401 0.1165 5.69e-02 0.00983 3.55e-01 0.014721 6.34e-03 6.00e-03
#> HERNU 0.39928 0.1551 2.73e-03 0.08870 1.79e-03 0.021248 3.58e-02 2.61e-01
#> BARRAS 0.61624 0.0333 8.48e-02 0.01024 1.07e-02 0.001594 9.13e-03 9.12e-02
#> NOOL 0.48987 0.1571 2.34e-02 0.15369 1.29e-01 0.015701 1.80e-02 1.19e-02
#> BOURGUIGNON 0.85970 0.0705 4.45e-06 0.01962 7.75e-03 0.000297 1.58e-02 1.40e-02
#> Sebrle 0.67538 0.0840 1.60e-01 0.03708 3.56e-05 0.000389 5.85e-06 5.30e-05
#> Clay 0.68759 0.1648 2.39e-02 0.00627 2.03e-02 0.037763 4.15e-03 2.11e-02
#> Karpov 0.78367 0.0301 4.87e-02 0.00464 3.01e-02 0.005138 8.80e-02 5.64e-03
#> Macey 0.36344 0.4531 1.02e-01 0.03636 4.95e-09 0.004140 7.71e-03 1.40e-02
#> Warners 0.25565 0.0106 5.31e-01 0.13808 2.18e-04 0.041169 9.50e-03 1.59e-03
#> Zsivoczky 0.04505 0.1740 6.05e-01 0.00692 3.36e-02 0.002625 3.23e-04 5.87e-02
#> Hernu 0.02482 0.4418 9.46e-03 0.23420 1.55e-01 0.035771 6.38e-02 1.99e-02
#> Bernard 0.28935 0.3381 1.07e-01 0.08598 1.14e-01 0.016659 2.05e-02 5.88e-06
#> Schwarzl 0.11672 0.1003 2.51e-01 0.19889 1.93e-02 0.109806 7.40e-02 1.09e-01
#> Pogorelov 0.00780 0.1259 1.50e-02 0.31210 3.85e-05 0.431416 1.04e-01 2.40e-04
#> Schoenbeck 0.06707 0.4620 2.90e-03 0.01699 1.14e-01 0.007150 2.01e-01 1.79e-02
#> Barras 0.01897 0.1277 1.41e-01 0.06604 1.16e-01 0.262130 1.70e-01 2.54e-02
#> Dim.9 Dim.10
#> SEBRLE 8.95e-02 0.000221
#> CLAY 2.82e-04 0.007847
#> BERNARD 3.23e-03 0.001096
#> YURKOV 1.53e-03 0.001822
#> ZSIVOCZKY 3.85e-02 0.017092
#> McMULLEN 1.73e-03 0.023927
#> MARTINEAU 3.52e-03 0.026821
#> HERNU 4.27e-06 0.034229
#> BARRAS 8.77e-02 0.055153
#> NOOL 8.51e-04 0.000588
#> BOURGUIGNON 1.22e-02 0.000151
#> Sebrle 4.07e-02 0.002737
#> Clay 1.05e-02 0.023726
#> Karpov 1.76e-03 0.002232
#> Macey 1.44e-02 0.004803
#> Warners 4.32e-03 0.007784
#> Zsivoczky 6.96e-02 0.004127
#> Hernu 1.46e-03 0.014160
#> Bernard 1.21e-02 0.015917
#> Schwarzl 1.62e-05 0.021117
#> Pogorelov 2.89e-03 0.000232
#> Schoenbeck 8.70e-02 0.024083
#> Barras 1.99e-03 0.0711843.6 Predict using PCA
In this section, we’ll show how to predict the coordinates of supplementary individuals and variables using only the information provided by the previously performed PCA.
- Data: rows 24 to 27 and columns 1 to to 10 [in decathlon2 data sets]. The new data must contain columns (variables) with the same names and in the same order as the active data used to compute PCA.
# Data for the supplementary individuals
ind.sup <- decathlon2[24:27, 1:10]
ind.sup[, 1:6]
#> X100m Long.jump Shot.put High.jump X400m X110m.hurdle
#> KARPOV 11.0 7.30 14.8 2.04 48.4 14.1
#> WARNERS 11.1 7.60 14.3 1.98 48.7 14.2
#> Nool 10.8 7.53 14.3 1.88 48.8 14.8
#> Drews 10.9 7.38 13.1 1.88 48.5 14.0- Predict the coordinates of new individuals data. Use the R base function predict():
ind.sup.coord <- predict(res.pca, newdata = ind.sup)
ind.sup.coord[, 1:4]
#> PC1 PC2 PC3 PC4
#> KARPOV 0.777 -0.762 1.597 1.686
#> WARNERS -0.378 0.119 1.701 -0.691
#> Nool -0.547 -1.934 0.472 -2.228
#> Drews -1.085 -0.017 2.982 -1.501- Graph of individuals including the supplementary individuals:
# Plot of active individuals
p <- fviz_pca_ind(res.pca, repel = TRUE)
# Add supplementary individuals
fviz_add(p, ind.sup.coord, color ="blue")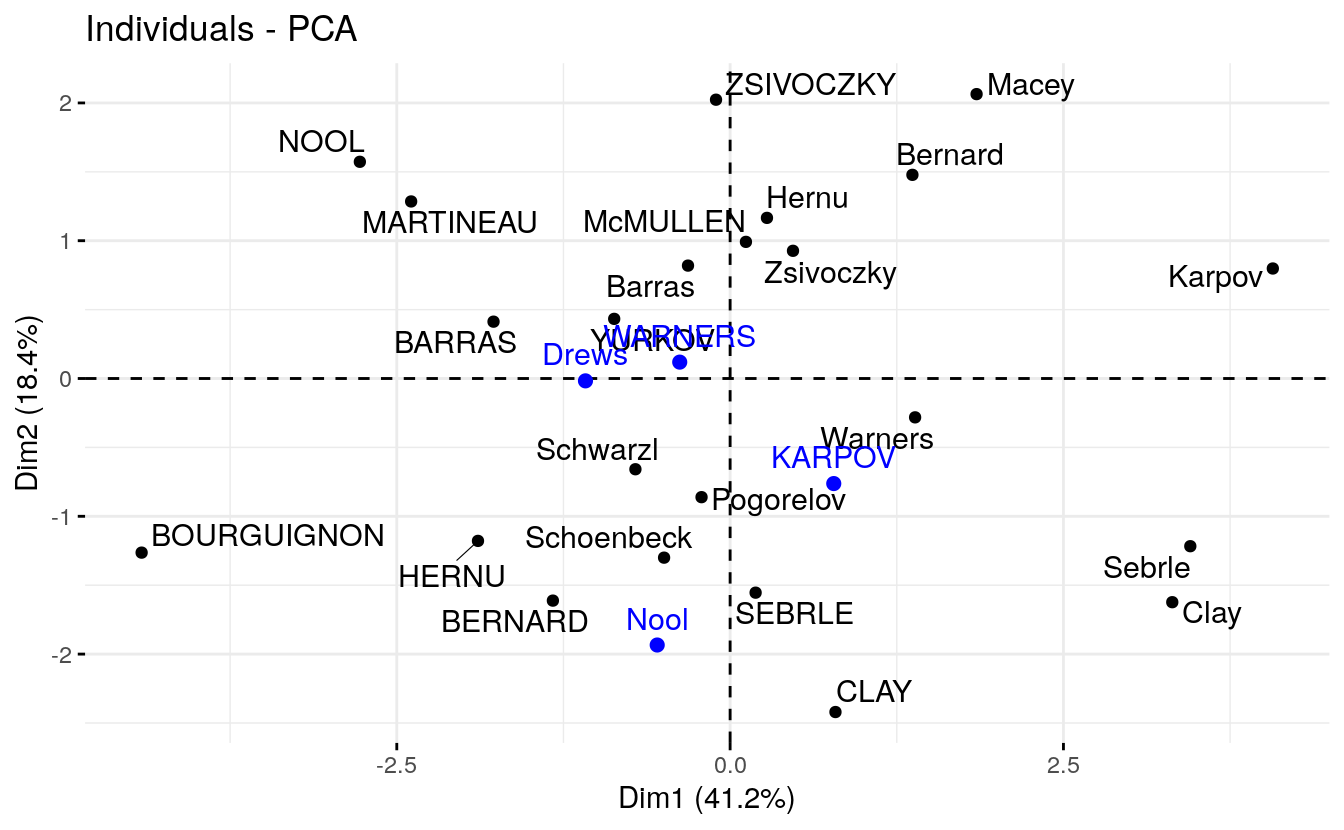
The predicted coordinates of individuals can be manually calculated as follow:
- Center and scale the new individuals data using the center and the scale of the PCA
- Calculate the predicted coordinates by multiplying the scaled values with the eigenvectors (loadings) of the principal components. The R code below can be used :
# Centering and scaling the supplementary individuals
ind.scaled <- scale(ind.sup,
center = res.pca$center,
scale = res.pca$scale)
# Coordinates of the individividuals
coord_func <- function(ind, loadings){
r <- loadings*ind
apply(r, 2, sum)
}
pca.loadings <- res.pca$rotation
ind.sup.coord <- t(apply(ind.scaled, 1, coord_func, pca.loadings ))
ind.sup.coord[, 1:4]
#> PC1 PC2 PC3 PC4
#> KARPOV 0.777 -0.762 1.597 1.686
#> WARNERS -0.378 0.119 1.701 -0.691
#> Nool -0.547 -1.934 0.472 -2.228
#> Drews -1.085 -0.017 2.982 -1.5013.7 Supplementary variables
3.7.1 Qualitative / categorical variables
The data sets decathlon2 contain a supplementary qualitative variable at columns 13 corresponding to the type of competitions.
Qualitative / categorical variables can be used to color individuals by groups. The grouping variable should be of same length as the number of active individuals (here 23).
groups <- as.factor(decathlon2$Competition[1:23])
fviz_pca_ind(res.pca,
col.ind = groups, # color by groups
palette = c("#00AFBB", "#FC4E07"),
addEllipses = TRUE, # Concentration ellipses
ellipse.type = "confidence",
legend.title = "Groups",
repel = TRUE
)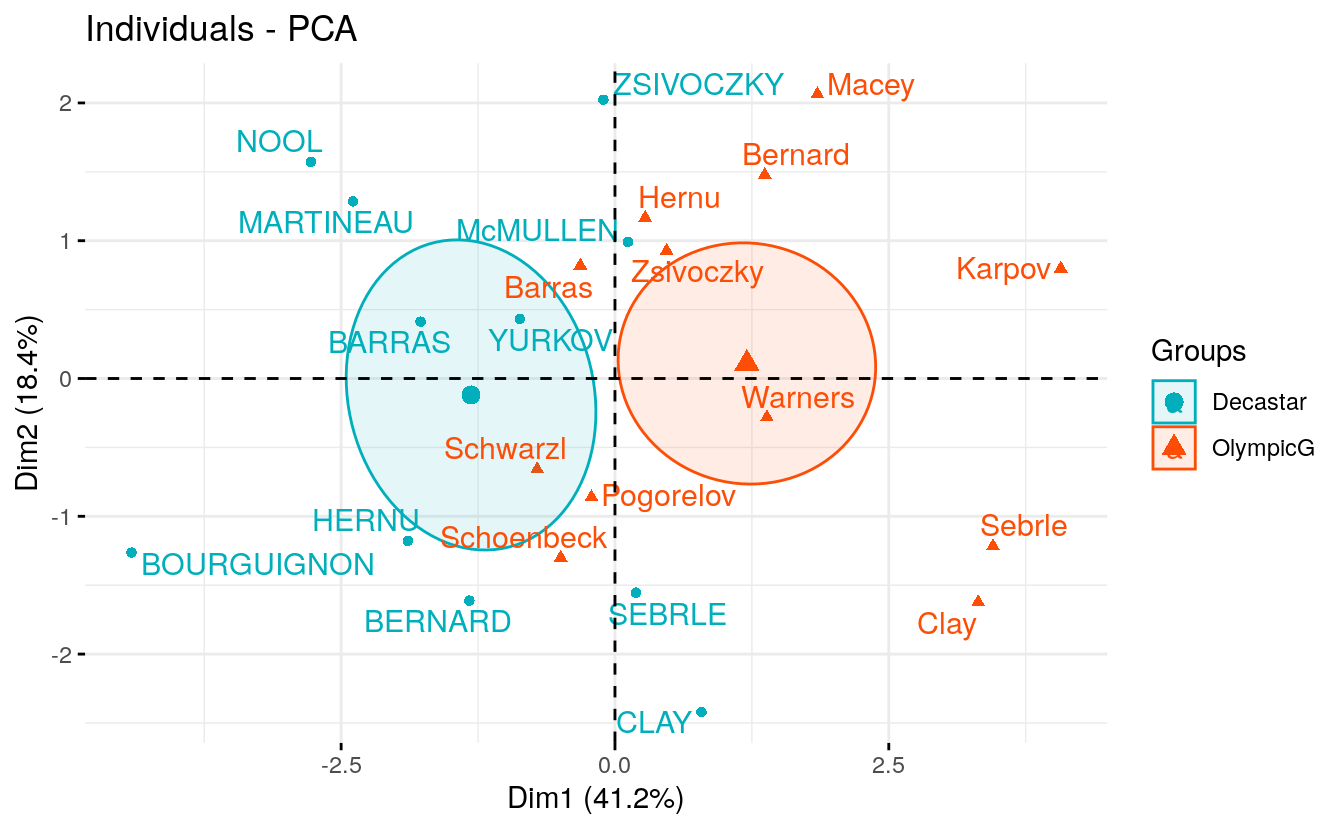
Calculate the coordinates for the levels of grouping variables. The coordinates for a given group is calculated as the mean coordinates of the individuals in the group.
library(magrittr) # for pipe %>%
library(dplyr) # everything else
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
# 1. Individual coordinates
res.ind <- get_pca_ind(res.pca)
# 2. Coordinate of groups
coord.groups <- res.ind$coord %>%
as_data_frame() %>%
select(Dim.1, Dim.2) %>%
mutate(competition = groups) %>%
group_by(competition) %>%
summarise(
Dim.1 = mean(Dim.1),
Dim.2 = mean(Dim.2)
)
#> Warning: `as_data_frame()` is deprecated as of tibble 2.0.0.
#> Please use `as_tibble()` instead.
#> The signature and semantics have changed, see `?as_tibble`.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_warnings()` to see where this warning was generated.
coord.groups
#> # A tibble: 2 x 3
#> competition Dim.1 Dim.2
#> <fct> <dbl> <dbl>
#> 1 Decastar -1.31 -0.119
#> 2 OlympicG 1.20 0.1093.7.2 Quantitative variables
Data: columns 11:12. Should be of same length as the number of active individuals (here 23)
quanti.sup <- decathlon2[1:23, 11:12, drop = FALSE]
head(quanti.sup)
#> Rank Points
#> SEBRLE 1 8217
#> CLAY 2 8122
#> BERNARD 4 8067
#> YURKOV 5 8036
#> ZSIVOCZKY 7 8004
#> McMULLEN 8 7995The coordinates of a given quantitative variable are calculated as the correlation between the quantitative variables and the principal components.
# Predict coordinates and compute cos2
quanti.coord <- cor(quanti.sup, res.pca$x)
quanti.cos2 <- quanti.coord^2
# Graph of variables including supplementary variables
p <- fviz_pca_var(res.pca)
fviz_add(p, quanti.coord, color ="blue", geom="arrow")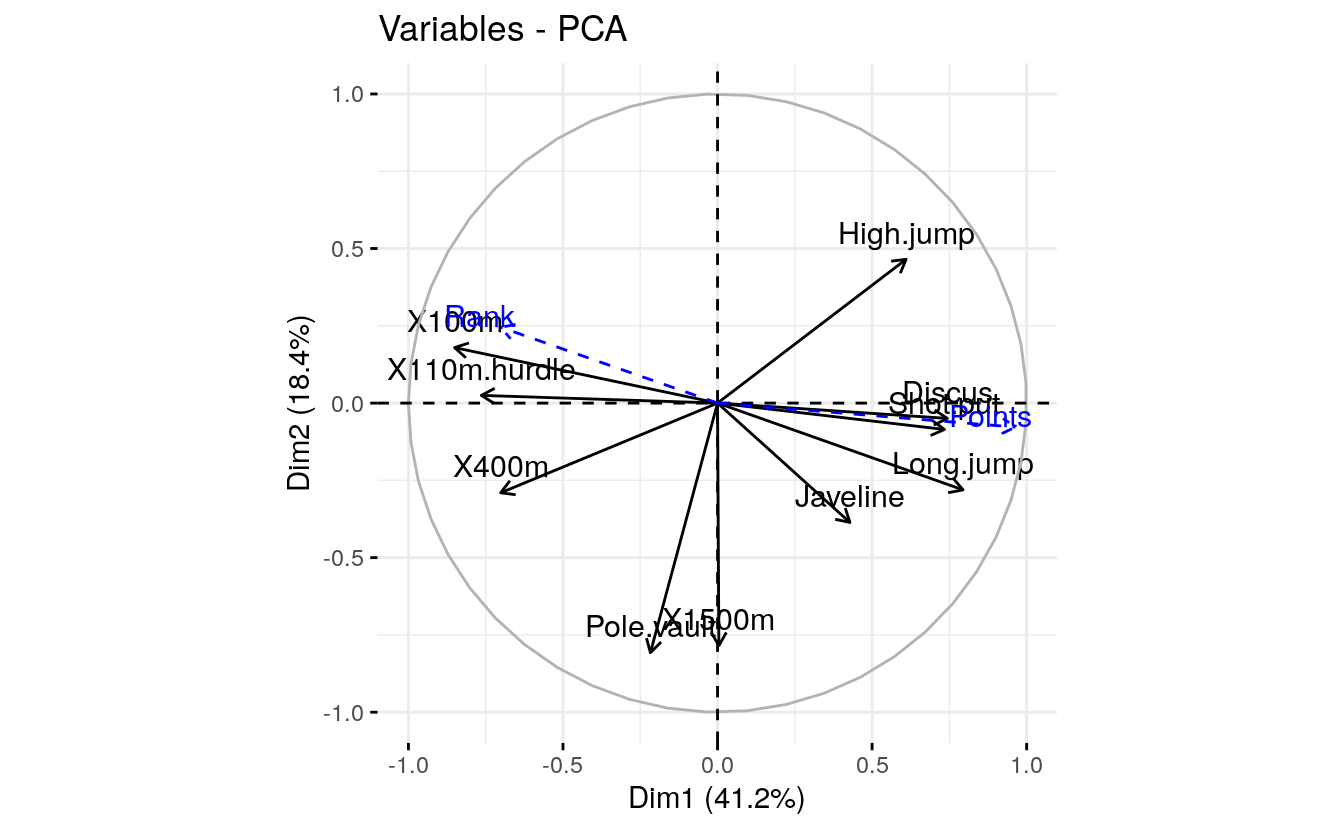
3.8 Theory behind PCA results
3.8.1 PCA results for variables
Here we’ll show how to calculate the PCA results for variables: coordinates, cos2 and contributions:
var.coord = loadings * the component standard deviations var.cos2 = var.coord^2 var.contrib. The contribution of a variable to a given principal component is (in percentage) : (var.cos2 * 100) / (total cos2 of the component)
# Helper function
#::::::::::::::::::::::::::::::::::::::::
var_coord_func <- function(loadings, comp.sdev){
loadings*comp.sdev
}
# Compute Coordinates
#::::::::::::::::::::::::::::::::::::::::
loadings <- res.pca$rotation
sdev <- res.pca$sdev
var.coord <- t(apply(loadings, 1, var_coord_func, sdev))
head(var.coord[, 1:4])
#> PC1 PC2 PC3 PC4
#> X100m -0.851 0.1794 -0.302 0.0336
#> Long.jump 0.794 -0.2809 0.191 -0.1154
#> Shot.put 0.734 -0.0854 -0.518 0.1285
#> High.jump 0.610 0.4652 -0.330 0.1446
#> X400m -0.702 -0.2902 -0.284 0.4308
#> X110m.hurdle -0.764 0.0247 -0.449 -0.0169
# Compute Cos2
#::::::::::::::::::::::::::::::::::::::::
var.cos2 <- var.coord^2
head(var.cos2[, 1:4])
#> PC1 PC2 PC3 PC4
#> X100m 0.724 0.032184 0.0909 0.001127
#> Long.jump 0.631 0.078881 0.0363 0.013315
#> Shot.put 0.539 0.007294 0.2679 0.016504
#> High.jump 0.372 0.216424 0.1090 0.020895
#> X400m 0.492 0.084203 0.0804 0.185611
#> X110m.hurdle 0.584 0.000612 0.2015 0.000285
# Compute contributions
#::::::::::::::::::::::::::::::::::::::::
comp.cos2 <- apply(var.cos2, 2, sum)
contrib <- function(var.cos2, comp.cos2){var.cos2*100/comp.cos2}
var.contrib <- t(apply(var.cos2,1, contrib, comp.cos2))
head(var.contrib[, 1:4])
#> PC1 PC2 PC3 PC4
#> X100m 17.54 1.7505 7.34 0.1376
#> Long.jump 15.29 4.2904 2.93 1.6249
#> Shot.put 13.06 0.3967 21.62 2.0141
#> High.jump 9.02 11.7716 8.79 2.5499
#> X400m 11.94 4.5799 6.49 22.6509
#> X110m.hurdle 14.16 0.0333 16.26 0.03483.8.2 PCA results for individuals
ind.coord= res.pca$x-
Cos2 of individuals. Two steps:
- Calculate the square distance between each individual and the PCA center of gravity: d2 = [(var1_ind_i - mean_var1)/sd_var1]^2 + …+ [(var10_ind_i - mean_var10)/sd_var10]^2 + …+..
- Calculate the cos2 as ind.coord^2/d2
Contributions of individuals to the principal components: 100 * (1 / number_of_individuals)*(ind.coord^2 / comp_sdev^2). Note that the sum of all the contributions per column is 100
# Coordinates of individuals
#::::::::::::::::::::::::::::::::::
ind.coord <- res.pca$x
head(ind.coord[, 1:4])
#> PC1 PC2 PC3 PC4
#> SEBRLE 0.191 -1.554 -0.628 0.0821
#> CLAY 0.790 -2.420 1.357 1.2698
#> BERNARD -1.329 -1.612 -0.196 -1.9209
#> YURKOV -0.869 0.433 -2.474 0.6972
#> ZSIVOCZKY -0.106 2.023 1.305 -0.0993
#> McMULLEN 0.119 0.992 0.844 1.3122
# Cos2 of individuals
#:::::::::::::::::::::::::::::::::
# 1. square of the distance between an individual and the
# PCA center of gravity
center <- res.pca$center
scale<- res.pca$scale
getdistance <- function(ind_row, center, scale){
return(sum(((ind_row-center)/scale)^2))
}
d2 <- apply(decathlon2.active,1, getdistance, center, scale)
# 2. Compute the cos2. The sum of each row is 1
cos2 <- function(ind.coord, d2){return(ind.coord^2/d2)}
ind.cos2 <- apply(ind.coord, 2, cos2, d2)
head(ind.cos2[, 1:4])
#> PC1 PC2 PC3 PC4
#> SEBRLE 0.00753 0.4975 0.08133 0.00139
#> CLAY 0.04870 0.4570 0.14363 0.12579
#> BERNARD 0.19720 0.2900 0.00429 0.41182
#> YURKOV 0.09611 0.0238 0.77823 0.06181
#> ZSIVOCZKY 0.00157 0.5764 0.23975 0.00139
#> McMULLEN 0.00218 0.1522 0.11014 0.26649
# Contributions of individuals
#:::::::::::::::::::::::::::::::
contrib <- function(ind.coord, comp.sdev, n.ind){
100*(1/n.ind)*ind.coord^2/comp.sdev^2
}
ind.contrib <- t(apply(ind.coord, 1, contrib,
res.pca$sdev, nrow(ind.coord)))
head(ind.contrib[, 1:4])
#> PC1 PC2 PC3 PC4
#> SEBRLE 0.0385 5.712 1.385 0.0357
#> CLAY 0.6581 13.854 6.460 8.5557
#> BERNARD 1.8627 6.144 0.135 19.5783
#> YURKOV 0.7969 0.443 21.476 2.5794
#> ZSIVOCZKY 0.0118 9.682 5.975 0.0523
#> McMULLEN 0.0148 2.325 2.497 9.1353