The goal of rODE is to explore R and its S4 classes and its differences with Java and Python classes while exploring physics simulations by solving ordinary differential equations (ODE).
Motivation
This is not your typical black-box ODE solver. You really have to develop your ODE algorithm using any of the ODE solvers available in the package. The objective is learning while coding R, understanding the physics and using the math.
rODE has been inspired on the extraordinary physics library for computer simulations OpenSourcePhyisics. Take a look at it at http://opensourcephysics.org. I highly recommend the book An Introduction to Computer Simulation Methods: Applications To Physical Systems, (Gould, Tobochnik, and Christian, 2017). It has helped me a lot in understanding the physics behind ordinary differential equations. The book briliantly combines code, algorithms, math and physics.
Additionally I have consulted these sources during the developing of the package rODE:
- The beatiful introduction to computers and numerical methods for petroleum engineering “Using the Computer to Solve Petroleum Engineering Problems” by Melvin Nobles“,
(Nobles, 1974) - Some examples and analytical solutions were borrowed from “Numerical Solution of Ordinary Differential Equations”,
(Atkinson, Han, and Stewart, 2009). - The paper “Numerical Reservoir Simulation Using an Ordinary-Differential-Equations Integrator”,
(Sincovec, 1975). - The thesis “Numerical Methods For Solution of Differential Equations”,
(Ritschel, 2013). - The paper “On Dormand-Prince Method” where I could learn about the Dormand-Prince ODE solver,
(Kimura, 2009). - The paper “A Family of Embedded Runge-Kutta formulae”,
(Dormand and Prince, 1980), where you can see the derivation of the ODE solverRK-45. - The paper on solving ODEs in R
(Soetaert, Petzoldt, and Setzer, 2010). - The paper “Behind and beyond the Matlab ODE suite”
(Ashino, Nagase, and Vaillancourt, 2000).
ODE solvers in this package
The ODE solvers implemented in R so far:
- Euler
- Euler-Richardson
- Verlet
- RK4
- RK45, Dormand-Prince45
Installation
You can install the latest development version of rODE from github with:
# install from the *develop* branch
devtools::install_github("f0nzie/rODE", ref = "develop")Or the stable version from CRAN:
install.packages("rODE")Examples
Example scripts are located under the folder examples inside the package.
These examples make use of a parent class containing a customized rate calculation as well as the step and startup method. The methods that you would commonly find in the base script or parent class are:
getRate()getState()-
step()ordoStep() setStepSize()-
init(), which is not the same as theS4classinitializemethod -
initialize(), and - the constructor
These methods are defined in the virtual classes ODE and ODESolver.
Two other classes that serve as definition classes for the ODE solvers are: AbstractODESolver and ODEAdaptiveSolver.
For instance, the application KeplerApp.R needs the class Kepler located in the Kepler.R script, which is called with planet <- Kepler(r, v), an ODE object. The solver for the same application is RK45 called with solver <- RK45(planet), where planet is a previuously declared ODE object. Since RK45 is an ODE solver, the script RK45.R will be located in the folder ./R in the package.
Vignettes
The vignettes contain examples of the use of the various ODE solvers.
For instance, the notebook Comparison and Kepler use the ODE solver RK45; FallingParticle and Planet use the Euler solver; Pendulum makes use of EulerRichardson; Planet of Euler, Projectile; Reaction of RK4, and KeplerEnergy uses the ODE solver Verlet.
Tests
There are tests for the core ODE solver classes under tests/testthat, as well as additional tests for the examples themselves.
Test this folder
The tests for the examples are two: one for the base/parent classes such as Kepler or Planet or Projectile; this test runner is called run_tests_this_folder.R.
For the applications there is another runner (run_test_applications.R) that opens each of the applications as request for a return value. If the hard coded value is not returned, the test will fail. This ensures that any minor change in the core solver classes do not have any impact on the application solutions, and if there is, it must be explained.
Tests all the application examples
You can test all applications under the examples folder by running the script run_test_applications.R. The way it works is by getting the list of all applications by filtering those ending with App. Then removes the extension .R from each app and starts looping to call each of the applications with do.call. A list contains the expected results that are compared against the result coming out from the call to the R application.
Applications
- AdaptiveStepApp
- ComparisonRK45App
- FallingParticleODE
- KeplerApp
- KeplerEnergyApp
- LogisticApp
- PendulumApp
- PlanetApp
- ProjectileApp
- ReactionApp
- RigidBodyNXFApp
- SHOApp
- SpringRK4App
- VanderpolApp
- VanderpolMuTimeControlApp
AdaptiveStepApp
library(rODE)
#>
#> Attaching package: 'rODE'
#> The following object is masked from 'package:stats':
#>
#> step
importFromExamples("AdaptiveStep.R")
# running function
AdaptiveStepApp <- function(verbose = FALSE) {
ode <- new("Impulse")
ode_solver <- RK45(ode)
ode_solver <- init(ode_solver, 0.1)
ode_solver <- setTolerance(ode_solver, 1.0e-4)
i <- 1; rowVector <- vector("list")
while (getState(ode)[1] < 12) {
rowVector[[i]] <- list(s1 = getState(ode)[1],
s2 = getState(ode)[2],
t = getState(ode)[3])
ode_solver <- step(ode_solver)
ode <- ode_solver@ode
i <- i + 1
}
return(data.table::rbindlist(rowVector))
}
# run application
solution <- AdaptiveStepApp()
plot(solution)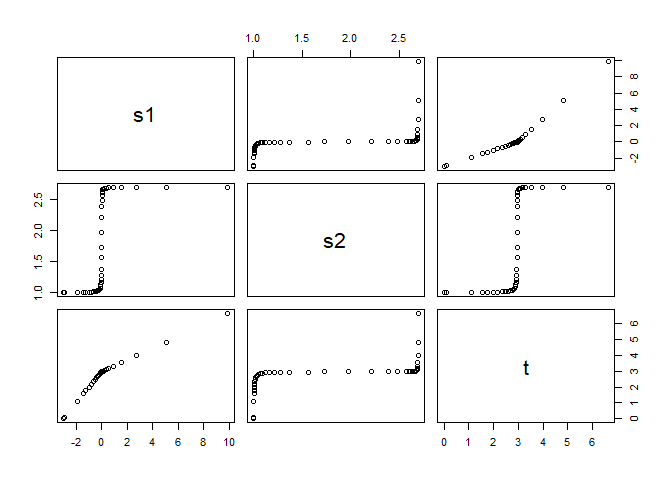
ComparisonRK45App
# ++++++++++++++++++++++++++++++++++++++++++++++++ example: ComparisonRK45App.R
# Compares the solution by the RK45 ODE solver versus the analytical solution
# Example file: ComparisonRK45App.R
# ODE Solver: Runge-Kutta 45
# Class: RK45
library(rODE)
importFromExamples("ODETest.R")
ComparisonRK45App <- function(verbose = FALSE) {
ode <- new("ODETest") # create an `ODETest` object
ode_solver <- RK45(ode) # select the ODE solver
ode_solver <- setStepSize(ode_solver, 1) # set the step
ode_solver <- setTolerance(ode_solver, 1e-8) # set the tolerance
rowVector <- vector("list")
time <- 0
i <- 1
while (time < 50) {
rowVector[[i]] <- list(t = ode_solver@ode@state[2],
s1 = getState(ode_solver@ode)[1],
s2 = getState(ode_solver@ode)[2],
xs = getExactSolution(ode_solver@ode, time),
rc = getRateCounts(ode),
time = time)
ode_solver <- step(ode_solver) # advance one step
stepSize <- ode_solver@stepSize # update the step size
time <- time + stepSize
state <- getState(ode_solver@ode) # get the `state` vector
i <- i + 1
}
return(data.table::rbindlist(rowVector)) # a data table with the results
}
# show solution
solution <- ComparisonRK45App() # run the example
plot(solution)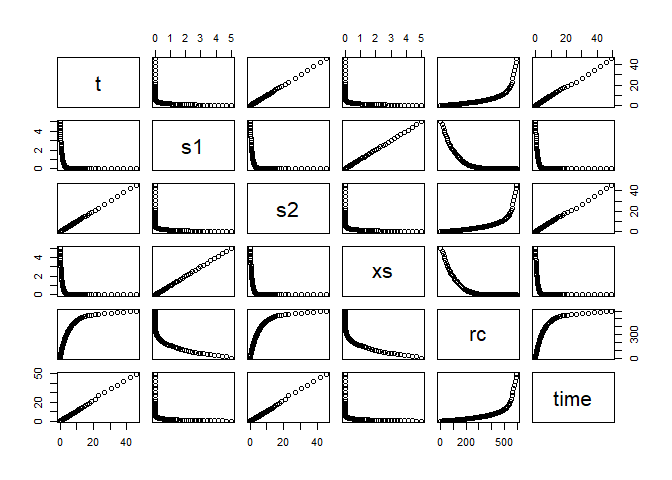
FallingParticleODE
# +++++++++++++++++++++++++++++++++++++++++++++++ example: FallingParticleApp.R
# Application that simulates the free fall of a ball using Euler ODE solver
library(rODE)
importFromExamples("FallingParticleODE.R") # source the class
FallingParticleODEApp <- function(verbose = FALSE) {
# initial values
initial_y <- 10
initial_v <- 0
dt <- 0.01
ball <- FallingParticleODE(initial_y, initial_v)
solver <- Euler(ball) # set the ODE solver
solver <- setStepSize(solver, dt) # set the step
rowVector <- vector("list")
i <- 1
# stop loop when the ball hits the ground, state[1] is the vertical position
while (ball@state[1] > 0) {
rowVector[[i]] <- list(t = ball@state[3],
y = ball@state[1],
vy = ball@state[2])
solver <- step(solver) # move one step at a time
ball <- solver@ode # update the ball state
i <- i + 1
}
DT <- data.table::rbindlist(rowVector)
return(DT)
}
# show solution
solution <- FallingParticleODEApp()
plot(solution)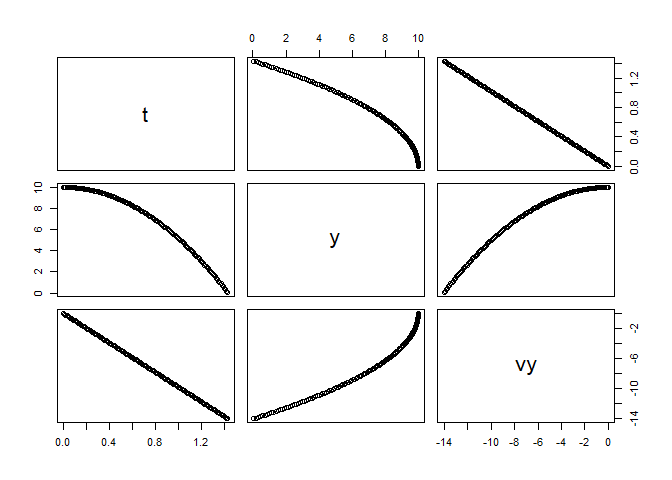
KeplerApp
# +++++++++++++++++++++++++++++++++++++++++++++++++++++++++ example KeplerApp.R
# KeplerApp solves an inverse-square law model (Kepler model) using an adaptive
# stepsize algorithm.
# Application showing two planet orbiting
# File in examples: KeplerApp.R
library(rODE)
importFromExamples("Kepler.R") # source the class Kepler
KeplerApp <- function(verbose = FALSE) {
# set the orbit into a predefined state.
r <- c(2, 0) # orbit radius
v <- c(0, 0.25) # velocity
dt <- 0.1
planet <- Kepler(r, v)
solver <- RK45(planet)
rowVector <- vector("list")
i <- 1
while (planet@state[5] <= 10) {
rowVector[[i]] <- list(t = planet@state[5],
planet1.r = planet@state[1],
p1anet1.v = planet@state[2],
planet2.r = planet@state[3],
p1anet2.v = planet@state[4])
solver <- step(solver)
planet <- solver@ode
i <- i + 1
}
DT <- data.table::rbindlist(rowVector)
return(DT)
}
solution <- KeplerApp()
plot(solution)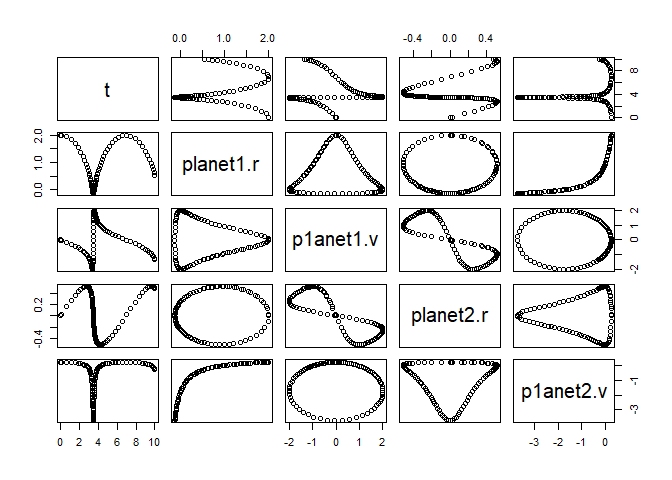
KeplerEnergyApp
# ++++++++++++++++++++++++++++++++++++++++++++++++++ example: KeplerEnergyApp.R
# Demostration of the use of the Verlet ODE solver
#
library(rODE)
importFromExamples("KeplerEnergy.R") # source the class Kepler
KeplerEnergyApp <- function(verbose = FALSE) {
# initial values
x <- 1
vx <- 0
y <- 0
vy <- 2 * pi
dt <- 0.01
tol <- 1e-3
particle <- KeplerEnergy()
particle <- init(particle, c(x, vx, y, vy, 0))
odeSolver <- Verlet(particle)
odeSolver <- init(odeSolver, dt)
particle@odeSolver <- odeSolver
initialEnergy <- getEnergy(particle)
rowVector <- vector("list")
i <- 1
while (getTime(particle) <= 1.20) {
rowVector[[i]] <- list(t = particle@state[5],
x = particle@state[1],
vx = particle@state[2],
y = particle@state[3],
vy = particle@state[4],
E = getEnergy(particle))
particle <- doStep(particle)
energy <- getEnergy(particle)
i <- i + 1
}
DT <- data.table::rbindlist(rowVector)
return(DT)
}
solution <- KeplerEnergyApp()
plot(solution)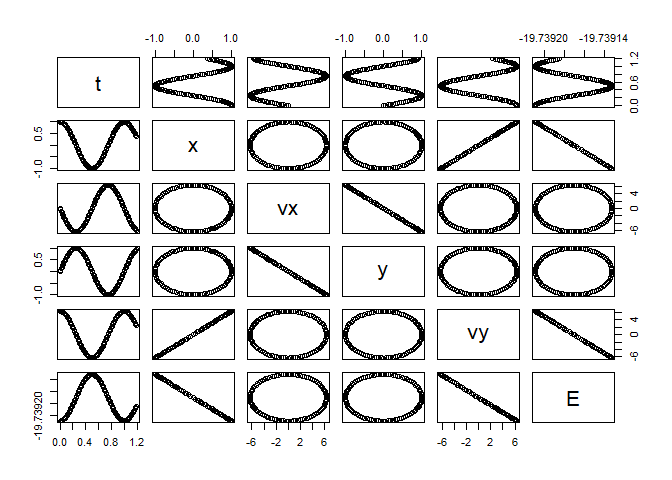
LogisticApp
library(rODE)
importFromExamples("Logistic.R") # source the class Logistic
# Run the application
LogisticApp <- function(verbose = FALSE) {
x <- 0.1
vx <- 0
r <- 2 # Malthusian parameter (rate of maximum population growth)
K <- 10.0 # carrying capacity of the environment
dt <- 0.01; tol <- 1e-3; tmax <- 10
population <- Logistic()
population <- init(population, c(x, vx, 0), r, K)
odeSolver <- Verlet(population)
odeSolver <- init(odeSolver, dt)
population@odeSolver <- odeSolver
rowVector <- vector("list")
i <- 1
while (getTime(population) <= tmax) {
rowVector[[i]] <- list(t = getTime(population),
s1 = population@state[1],
s2 = population@state[2])
population <- doStep(population)
i <- i + 1
}
DT <- data.table::rbindlist(rowVector)
return(DT)
}
# show solution
solution <- LogisticApp()
plot(solution)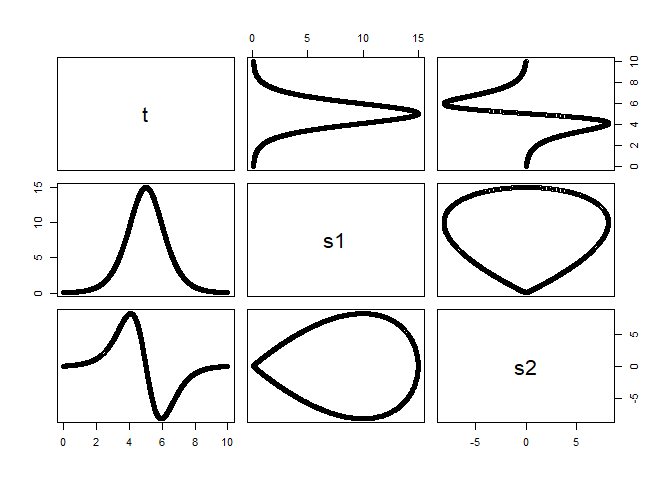
PendulumApp
# ++++++++++++++++++++++++++++++++++++++++++++++++++ example: PendulumApp.R
# Simulation of a pendulum using the EulerRichardson ODE solver
library(rODE)
suppressPackageStartupMessages(library(ggplot2))
importFromExamples("Pendulum.R") # source the class
PendulumApp <- function(verbose = FALSE) {
# initial values
theta <- 0.2
thetaDot <- 0
dt <- 0.1
ode <- new("ODE")
pendulum <- Pendulum()
pendulum@state[3] <- 0 # set time to zero, t = 0
pendulum <- setState(pendulum, theta, thetaDot)
pendulum <- setStepSize(pendulum, dt = dt) # using stepSize in RK4
pendulum@odeSolver <- setStepSize(pendulum@odeSolver, dt) # set new step size
rowvec <- vector("list")
i <- 1
while (pendulum@state[3] <= 40) {
rowvec[[i]] <- list(t = pendulum@state[3], # time
theta = pendulum@state[1], # angle
thetadot = pendulum@state[2]) # derivative of angle
pendulum <- step(pendulum)
i <- i + 1
}
DT <- data.table::rbindlist(rowvec)
return(DT)
}
# show solution
solution <- PendulumApp()
plot(solution)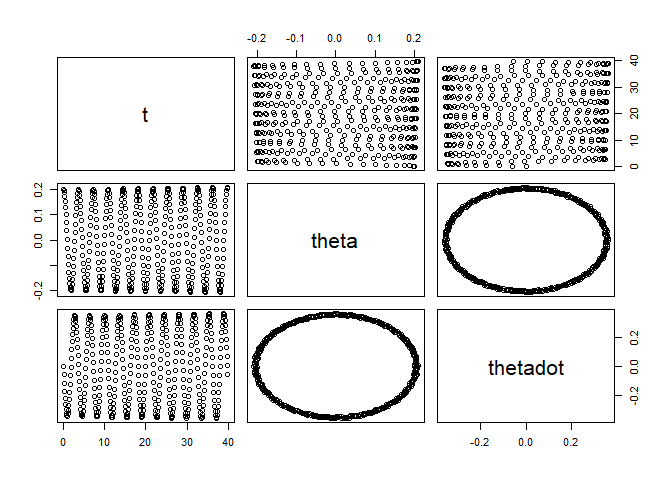
PlanetApp
# ++++++++++++++++++++++++++++++++++++++++++++++++++++++++ example: PlanetApp.R
# Simulation of Earth orbiting around the SUn using the Euler ODE solver
library(rODE)
importFromExamples("Planet.R") # source the class
PlanetApp <- function(verbose = FALSE) {
# x = 1, AU or Astronomical Units. Length of semimajor axis or the orbit
# of the Earth around the Sun.
x <- 1; vx <- 0; y <- 0; vy <- 6.28; t <- 0
state <- c(x, vx, y, vy, t)
dt <- 0.01
planet <- Planet()
planet@odeSolver <- setStepSize(planet@odeSolver, dt)
planet <- init(planet, initState = state)
rowvec <- vector("list")
i <- 1
# run infinite loop. stop with ESCAPE.
while (planet@state[5] <= 90) { # Earth orbit is 365 days around the sun
rowvec[[i]] <- list(t = planet@state[5], # just doing 3 months
x = planet@state[1], # to speed up for CRAN
vx = planet@state[2],
y = planet@state[3],
vy = planet@state[4])
for (j in 1:5) { # advances time
planet <- doStep(planet)
}
i <- i + 1
}
DT <- data.table::rbindlist(rowvec)
return(DT)
}
# run the application
solution <- PlanetApp()
select_rows <- seq(1, nrow(solution), 10) # do not overplot
solution <- solution[select_rows,]
plot(solution)
ProjectileApp
# +++++++++++++++++++++++++++++++++++++++++++++++++ application: ProjectileApp.R
# test Projectile with RK4
# originally uses Euler
library(rODE)
importFromExamples("Projectile.R") # source the class
ProjectileApp <- function(verbose = FALSE) {
# initial values
x <- 0; vx <- 10; y <- 0; vy <- 10
state <- c(x, vx, y, vy, 0) # state vector
dt <- 0.01
projectile <- Projectile()
projectile <- setState(projectile, x, vx, y, vy)
projectile@odeSolver <- init(projectile@odeSolver, 0.123)
projectile@odeSolver <- setStepSize(projectile@odeSolver, dt)
rowV <- vector("list")
i <- 1
while (projectile@state[3] >= 0) {
rowV[[i]] <- list(t = projectile@state[5],
x = projectile@state[1],
vx = projectile@state[2],
y = projectile@state[3], # vertical position
vy = projectile@state[4])
projectile <- step(projectile)
i <- i + 1
}
DT <- data.table::rbindlist(rowV)
return(DT)
}
solution <- ProjectileApp()
plot(solution)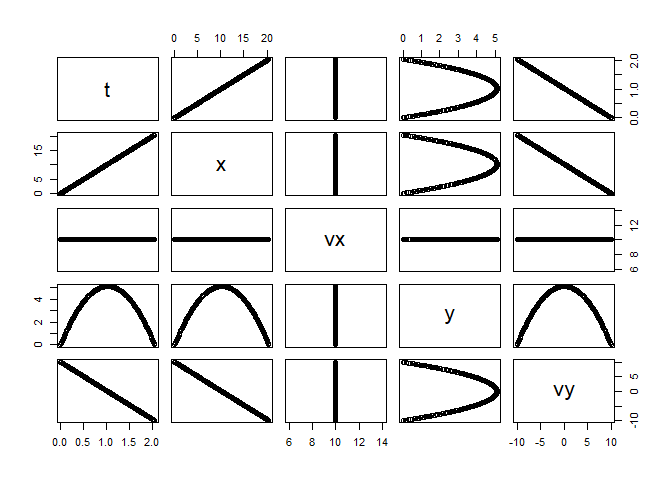
ReactionApp
# +++++++++++++++++++++++++++++++++++++++++++++++++++ application: ReactionApp.R
# ReactionApp solves an autocatalytic oscillating chemical
# reaction (Brusselator model) using
# a fourth-order Runge-Kutta algorithm.
library(rODE)
importFromExamples("Reaction.R") # source the class
ReactionApp <- function(verbose = FALSE) {
X <- 1; Y <- 5;
dt <- 0.1
reaction <- Reaction(c(X, Y, 0))
solver <- RK4(reaction)
rowvec <- vector("list")
i <- 1
while (solver@ode@state[3] < 100) { # stop at t = 100
rowvec[[i]] <- list(t = solver@ode@state[3],
X = solver@ode@state[1],
Y = solver@ode@state[2])
solver <- step(solver)
i <- i + 1
}
DT <- data.table::rbindlist(rowvec)
return(DT)
}
solution <- ReactionApp()
plot(solution)
RigidBodyNXFApp
# +++++++++++++++++++++++++++++++++++++++++++++++ application: RigidBodyNXFApp.R
# example of a nonstiff system is the system of equations describing
# the motion of a rigid body without external forces.
library(rODE)
importFromExamples("RigidBody.R")
# run the application
RigidBodyNXFApp <- function(verbose = FALSE) {
# load the R class that sets up the solver for this application
y1 <- 0 # initial y1 value
y2 <- 1 # initial y2 value
y3 <- 1 # initial y3 value
dt <- 0.01 # delta time for step
body <- RigidBodyNXF(y1, y2, y3)
solver <- Euler(body)
solver <- setStepSize(solver, dt)
rowVector <- vector("list")
i <- 1
# stop loop when the body hits the ground
while (body@state[4] <= 12) {
rowVector[[i]] <- list(t = body@state[4],
y1 = body@state[1],
y2 = body@state[2],
y3 = body@state[3])
solver <- step(solver)
body <- solver@ode
i <- i + 1
}
DT <- data.table::rbindlist(rowVector)
return(DT)
}
# get the data table from the app
solution <- RigidBodyNXFApp()
plot(solution)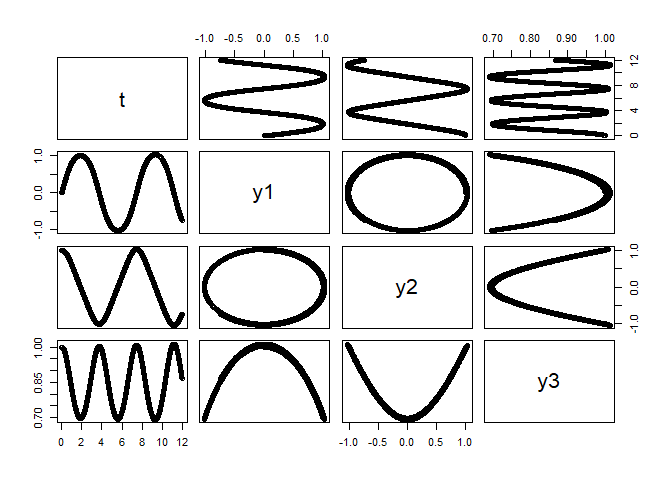
SHOApp
library(rODE)
importFromExamples("SHO.R")
# SHOApp.R
SHOApp <- function(...) {
x <- 1.0; v <- 0; k <- 1.0; dt <- 0.01; tolerance <- 1e-3
sho <- SHO(x, v, k)
solver_factory <- ODESolverFactory()
solver <- createODESolver(solver_factory, sho, "DormandPrince45")
# solver <- DormandPrince45(sho) # this can also be used
solver <- setTolerance(solver, tolerance)
solver <- init(solver, dt)
i <- 1; rowVector <- vector("list")
while (sho@state[3] <= 500) {
rowVector[[i]] <- list(x = sho@state[1],
v = sho@state[2],
t = sho@state[3])
solver <- step(solver)
sho <- solver@ode
i <- i + 1
}
return(data.table::rbindlist(rowVector))
}
solution <- SHOApp()
plot(solution)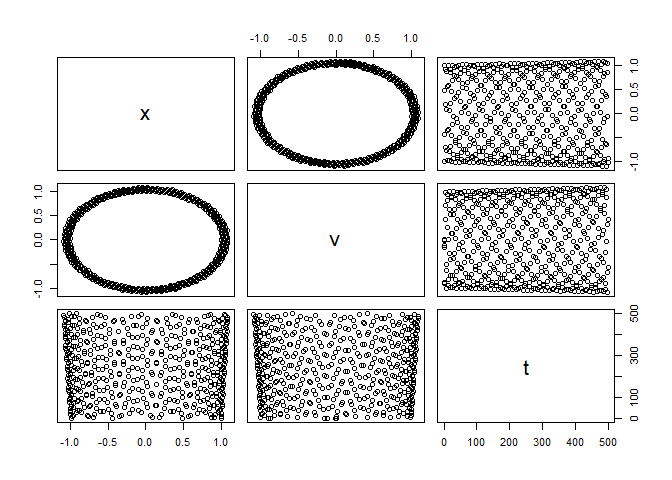
SpringRK4App
# ++++++++++++++++++++++++++++++++++++++++++++++++++application: SpringRK4App.R
# Simulation of a spring considering no friction
library(rODE)
importFromExamples("SpringRK4.R")
# run application
SpringRK4App <- function(verbose = FALSE) {
theta <- 0
thetaDot <- -0.2
tmax <- 22; dt <- 0.1
ode <- new("ODE")
spring <- SpringRK4()
spring@state[3] <- 0 # set time to zero, t = 0
spring <- setState(spring, theta, thetaDot)
spring <- setStepSize(spring, dt = dt) # using stepSize in RK4
spring@odeSolver <- setStepSize(spring@odeSolver, dt) # set new step size
rowvec <- vector("list")
i <- 1
while (spring@state[3] <= tmax) {
rowvec[[i]] <- list(t = spring@state[3], # angle
y1 = spring@state[1], # derivative of the angle
y2 = spring@state[2]) # time
i <- i + 1
spring <- step(spring)
}
DT <- data.table::rbindlist(rowvec)
return(DT)
}
# show solution
solution <- SpringRK4App()
plot(solution)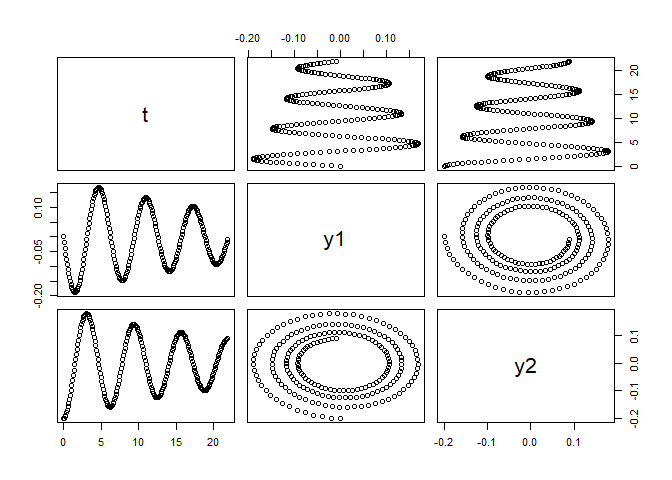
VanderpolApp
# ++++++++++++++++++++++++++++++++++++++++++++++++ application: VanderPolApp.R
# Solution of the Van der Pol equation
#
library(rODE)
importFromExamples("VanderPol.R")
# run the application
VanderpolApp <- function(verbose = FALSE) {
# set the orbit into a predefined state.
y1 <- 2; y2 <- 0; dt <- 0.1;
rigid_body <- VanderPol(y1, y2)
solver <- RK45(rigid_body)
rowVector <- vector("list")
i <- 1
while (rigid_body@state[3] <= 20) {
rowVector[[i]] <- list(t = rigid_body@state[3],
y1 = rigid_body@state[1],
y2 = rigid_body@state[2])
solver <- step(solver)
rigid_body <- solver@ode
i <- i + 1
}
DT <- data.table::rbindlist(rowVector)
return(DT)
}
# show solution
solution <- VanderpolApp()
plot(solution)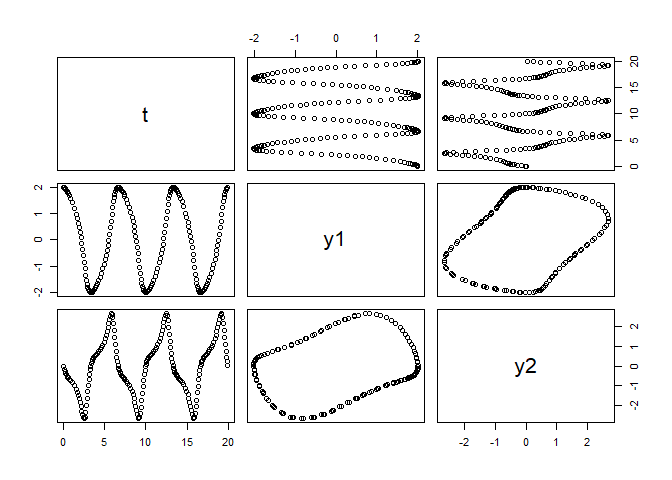
VanderpolMuTimeControlApp
# +++++++++++++++++++++++++++++++++++++ example: VanderpolMuTimeControlApp.R
# This is a modification of the original Vanderpol.R script
# In this version, we will add tha ability of setting mu and time lapse.
# This example is also shown in the Matlab help guide
library(rODE)
importFromExamples("VanderpolMuTimeControl.R")
# run the application
VanderpolMuTimeControlApp <- function(verbose = FALSE) {
# set the orbit into a predefined state.
y1 <- 2; y2 <- 0; mu <- 10; tmax <- mu * 3; dt <- 0.01
rigid_body <- VanderPol(y1, y2, mu)
solver <- RK45(rigid_body)
rowVector <- vector("list")
i <- 1
while (rigid_body@state[3] <= tmax) {
rowVector[[i]] <- list(t = rigid_body@state[3],
y1 = rigid_body@state[1],
y2 = rigid_body@state[2]
)
solver <- step(solver)
rigid_body <- solver@ode
i <- i + 1
}
DT <- data.table::rbindlist(rowVector)
return(DT)
}
# show solution
solution <- VanderpolMuTimeControlApp()
plot(solution)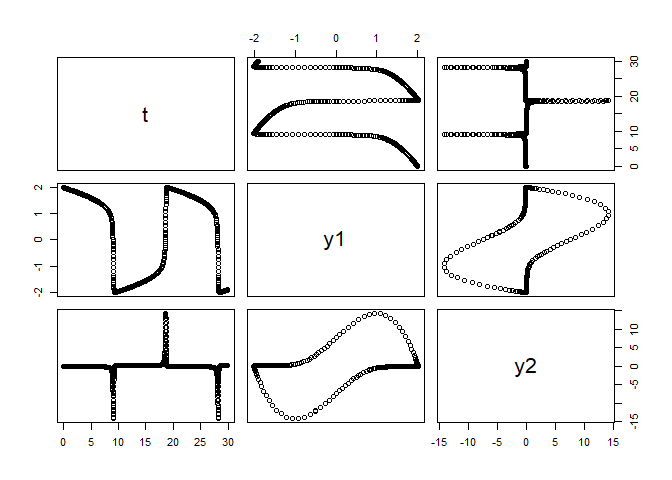
References
The following books and papers were consulted during the development of this package:
[1] R. Ashino, M. Nagase and R. Vaillancourt. “Behind and beyond the Matlab ODE suite”. In: Computers & Mathematics with Applications 40.4-5 (Aug. 2000), pp. 491-512. DOI: 10.1016/s0898-1221(00)00175-9.
[2] K. Atkinson, W. Han and D. E. Stewart. Numerical Solution of Ordinary Differential Equations. Wiley, 2009. ISBN: 978-0-470-04294-6.
[3] J. R. Dormand and P. J. Prince. “A family of embedded Runge-Kutta formulae”. In: Journal of computational and applied mathematics 6.1 (Mar. 1980), pp. 19-26. DOI: 10.1016/0771-050x(80)90013-3.
[4] H. Gould, J. Tobochnik and W. Christian. An Introduction to Computer Simulation Methods: Applications To Physical Systems. CreateSpace Independent Publishing Platform, 2017. ISBN: 978-1974427475.
[5] T. Kimura. “On dormand-prince method”. In: Retrieved April 27 (2009), p. 2014. <URL: http://depa.fquim.unam.mx/amyd/archivero/DormandPrince_19856.pdf>.
[6] M. A. Nobles. Using the Computer to Solve Petroleum Engineering Problems. Gulf Publishing Co, 1974. ISBN: 978-0872018860.
[7] T. Ritschel. “Numerical Methods For Solution of Dierential Equations”. Cand. thesis. DTU supervisor: John Bagterp Jørgensen, jbjo@dtu.dk, DTU Compute. Technical University of Denmark, Department of Applied Mathematics and Computer Science, 2013, p. 224. <URL: http://www.compute.dtu.dk/English.aspx>.
[8] R. Sincovec. “Numerical Reservoir Simulation Using an Ordinary-Differential-Equations Integrator”. In: Society of Petroleum Engineers Journal 15.03 (Jun. 1975), pp. 255-264. DOI: 10.2118/5104-pa.
[9] K. Soetaert, T. Petzoldt and R. W. Setzer. “Solving differential equations in R: package deSolve”. In: Journal of Statistical Software 33 (2010).