RK45 ODE solver class

RK45 ODE solver class

RK45 class constructor

RK45(ode)

Arguments

ode	and ODE object

Examples

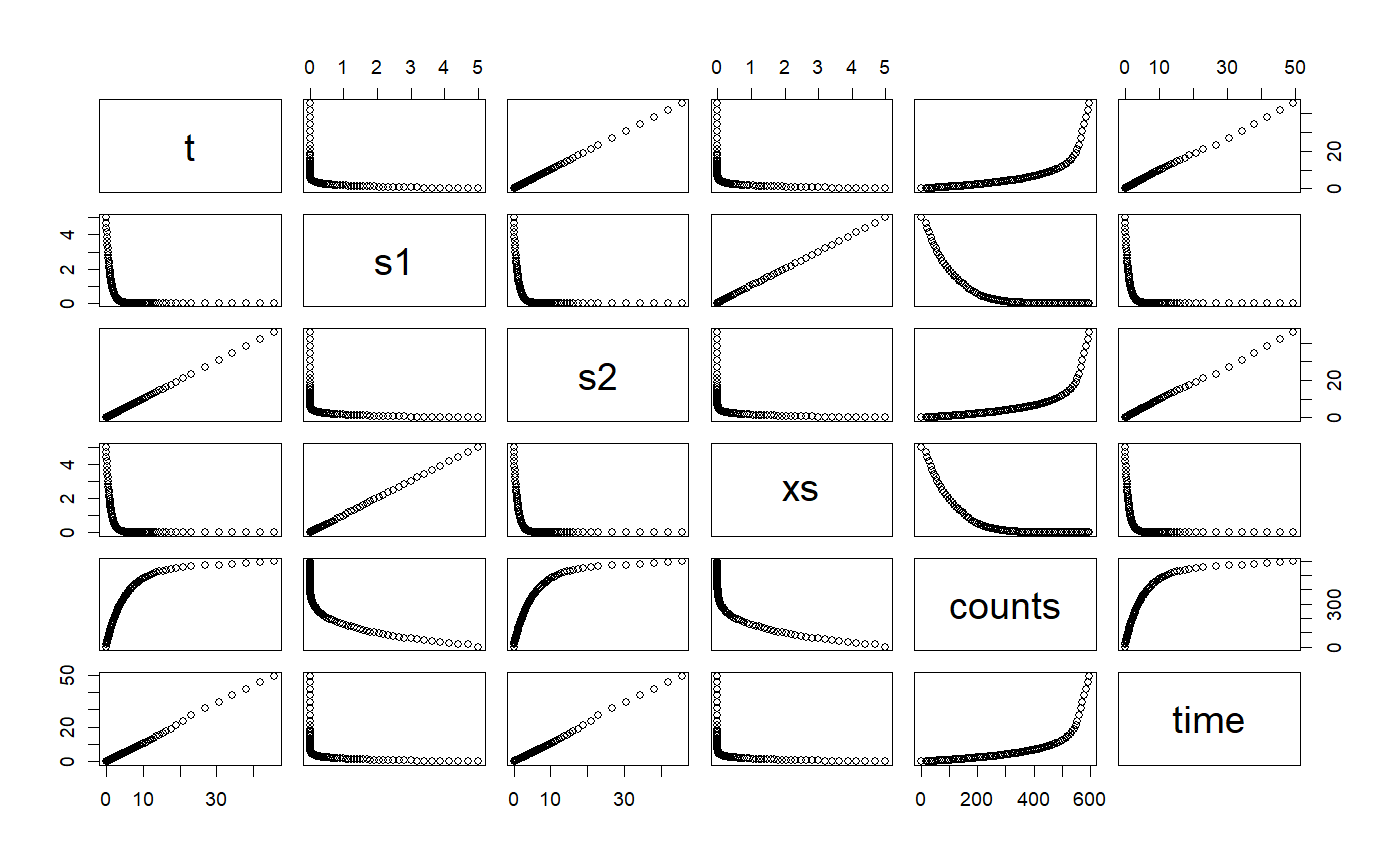
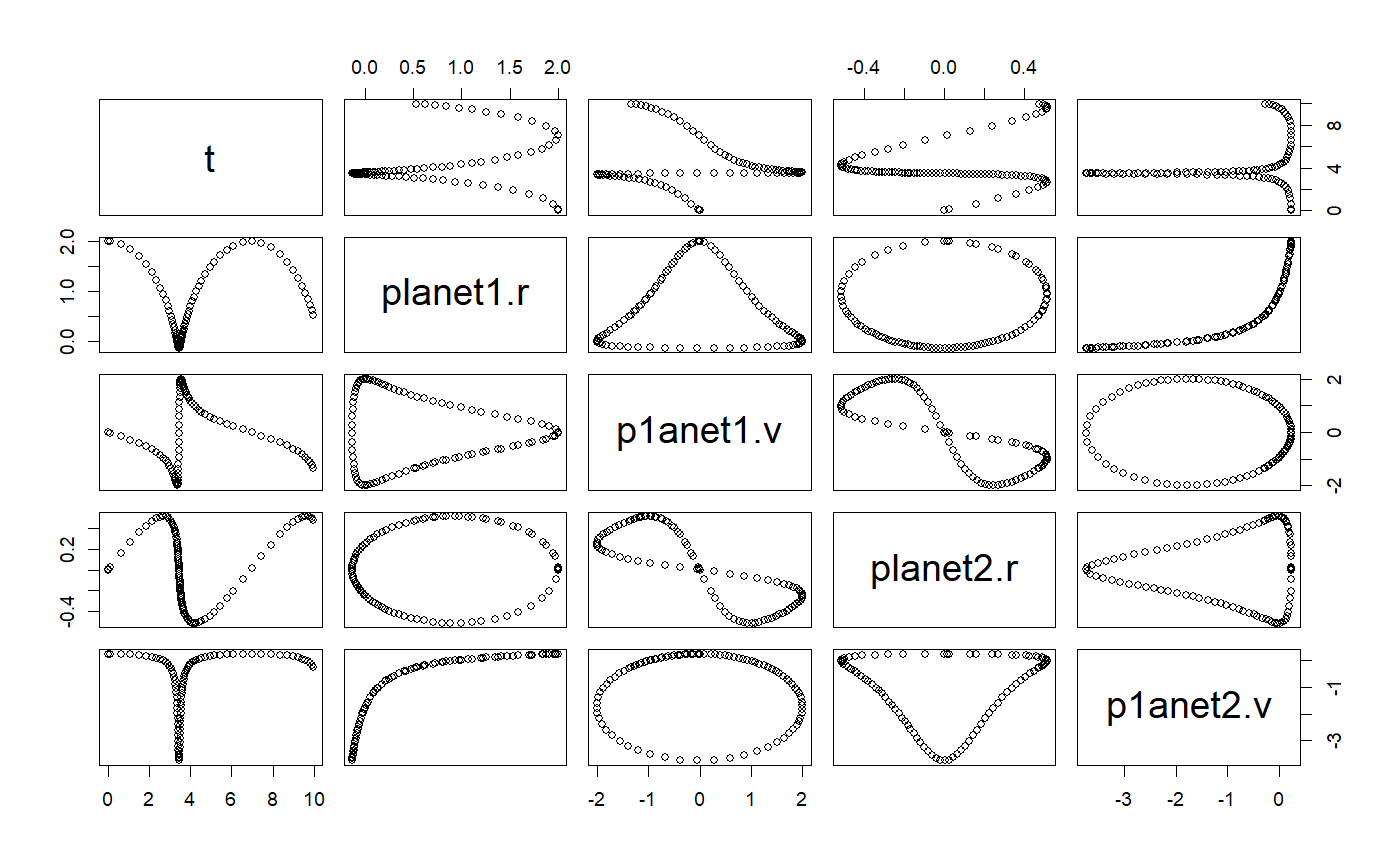
# ++++++++++++++++++++++++++++++++++++++++++++++++  example: ComparisonRK45App.R
# Compares the solution by the RK45 ODE solver versus the analytical solution
# Example file: ComparisonRK45App.R
# ODE Solver:   Runge-Kutta 45
# ODE class :   RK45
# Base class:   ODETest

importFromExamples("ODETest.R")

 ComparisonRK45App <- function(verbose = FALSE) {
     ode <- new("ODETest")                     # create an `ODETest` object
     ode_solver <- RK45(ode)                   # select the ODE solver
     ode_solver <- setStepSize(ode_solver, 1)      # set the step

     # Two ways of setting the tolerance
       # ode_solver <- setTolerance(ode_solver, 1e-8)  # set the tolerance
     setTolerance(ode_solver) <-  1e-8

     time <-  0
     rowVector <- vector("list")
     i <- 1
     while (time < 50) {
         rowVector[[i]] <- list(t  = getState(ode)[2],
                                s1 = getState(ode)[1],
                                s2 = getState(ode)[2],
                                xs = getExactSolution(ode, time),
                                counts = getRateCounts(ode),
                                time   = time
                                )
         ode_solver <- step(ode_solver)           # advance one step
         stepSize   <- getStepSize(ode_solver)
         time <- time + stepSize
         ode  <- getODE(ode_solver)                     # get updated ODE object
         i <- i + 1
     }
     return(data.table::rbindlist(rowVector))    # a data table with the results
 }
# show solution
solution <- ComparisonRK45App()                          # run the example
plot(solution)
#  +++++++++++++++++++++++++++++++++++++++++++++++++++++++++ example KeplerApp.R
#  KeplerApp solves an inverse-square law model (Kepler model) using an adaptive
#  stepsize algorithm.
#  Application showing two planet orbiting
#  File in examples: KeplerApp.R

importFromExamples("Kepler.R") # source the class Kepler

KeplerApp <- function(verbose = FALSE) {

    # set the orbit into a predefined state.
    r <- c(2, 0)                                   # orbit radius
    v <- c(0, 0.25)                                # velocity
    dt <- 0.1
    planet <- Kepler(r, v)                         # make up an ODE object
    solver <- RK45(planet)
    rowVector <- vector("list")
    i <- 1
    while (getState(planet)[5] <= 10) {
        rowVector[[i]] <- list(t  = planet@state[5],
                               planet1.r = getState(planet)[1],
                               p1anet1.v = getState(planet)[2],
                               planet2.r = getState(planet)[3],
                               p1anet2.v = getState(planet)[4])
        solver <- step(solver)
        planet <- getODE(solver)
        i <-  i + 1
    }
    DT <- data.table::rbindlist(rowVector)

    return(DT)
}

solution <- KeplerApp()
plot(solution)