Build the Projectile class with RK4 solver

library(rODE)
library(ggplot2)

####################
# This code can also be found in the `examples` folder under this name:
# 
# Projectile.R
#
# Projectile class to be solved with Euler method
#

setClass("Projectile", slots = c(
    g = "numeric",
    odeSolver = "RK4"
    ),
    prototype = prototype(
        g = 9.8
    ),
    contains = c("ODE")
    )

setMethod("initialize", "Projectile", function(.Object) {
    .Object@odeSolver <- RK4(.Object)
    return(.Object)
})

setMethod("setStepSize", "Projectile", function(object, stepSize, ...) {
    # use explicit parameter declaration
    # setStepSize generic has two step parameters: stepSize and dt
    object@odeSolver <- setStepSize(object@odeSolver, stepSize)
    object
})


setMethod("step", "Projectile", function(object) {
    object@odeSolver <- step(object@odeSolver)

    object@rate  <- object@odeSolver@ode@rate
    object@state <- object@odeSolver@ode@state

    object
})

setMethod("setState", signature("Projectile"), function(object, x, vx, y, vy, ...) {
    object@state[1] <- x
    object@state[2] <- vx
    object@state[3] <- y
    object@state[4] <- vy
    object@state[5] <- 0     # t + dt

    object@odeSolver@ode@state <- object@state
    object
})

setMethod("getState", "Projectile", function(object) {
    object@state
})


setMethod("getRate", "Projectile", function(object, state, ...) {
    object@rate[1] <- state[2]     # rate of change of x
    object@rate[2] <- 0            # rate of change of vx
    object@rate[3] <- state[4]     # rate of change of y
    object@rate[4] <- - object@g   # rate of change of vy
    object@rate[5] <- 1            # dt/dt = 1
    object@rate
})


# constructor
Projectile <- function()  new("Projectile")

## [1] "initialize"
## [1] "setStepSize"
## [1] "step"
## [1] "setState"
## [1] "getState"
## [1] "getRate"

Run the application ProjectileApp

# This code can also be found in the `examples` folder under this name:
#
# ProjectileApp.R
#                                                      test Projectile with RK4
#                                                      originally uses Euler
ProjectileApp <- function(verbose = FALSE) {
    library(data.table)
    
    x <- 0; vx <- 10; y <- 0; vy <- 10
    state <- c(x, vx, y, vy, 0)
    dt <- 0.01
    
    projectile <- Projectile()
    projectile <- setState(projectile, x, vx, y, vy)
    projectile@odeSolver <- init(projectile@odeSolver, 0.123)
    projectile@odeSolver <- setStepSize(projectile@odeSolver, dt)
    
    rowV <- vector("list")
    i <- 1
    while (projectile@state[3] >= 0)    {
        # state[5]:           state[1]: x;  # state[3]: y
        if (verbose)
            cat(sprintf("%12f %12f %12f \n", projectile@state[5],
                    projectile@state[1], projectile@state[3]))
        rowV[[i]] <- list(state1 = projectile@state[1],
                          state3 = projectile@state[3],
                          state5 = projectile@state[5])
        projectile <- step(projectile)
        i <- i + 1
    }
    
    datatable <- data.table::rbindlist(rowV)
    datatable
    
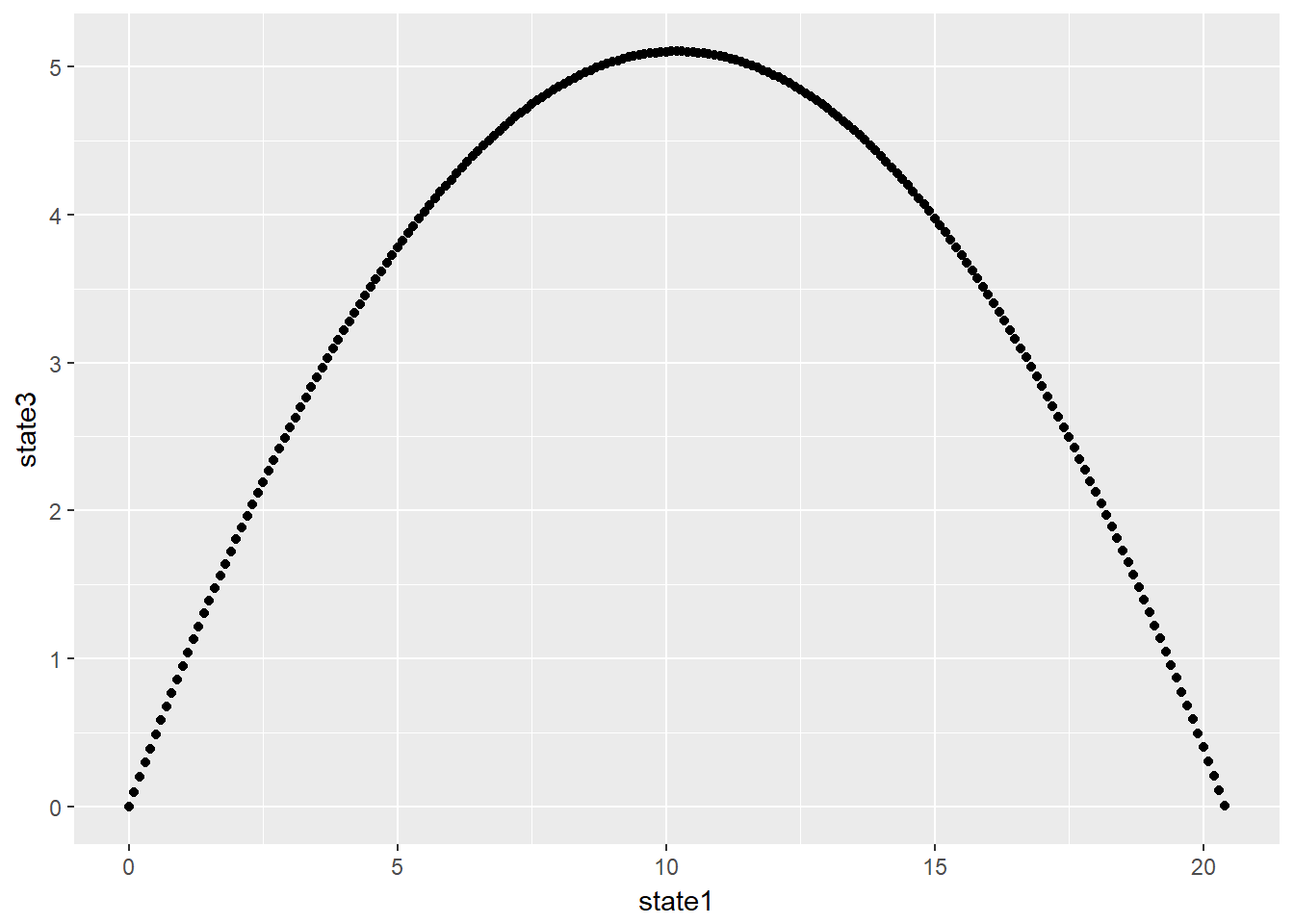
    print(qplot(state1, state3, data = datatable))
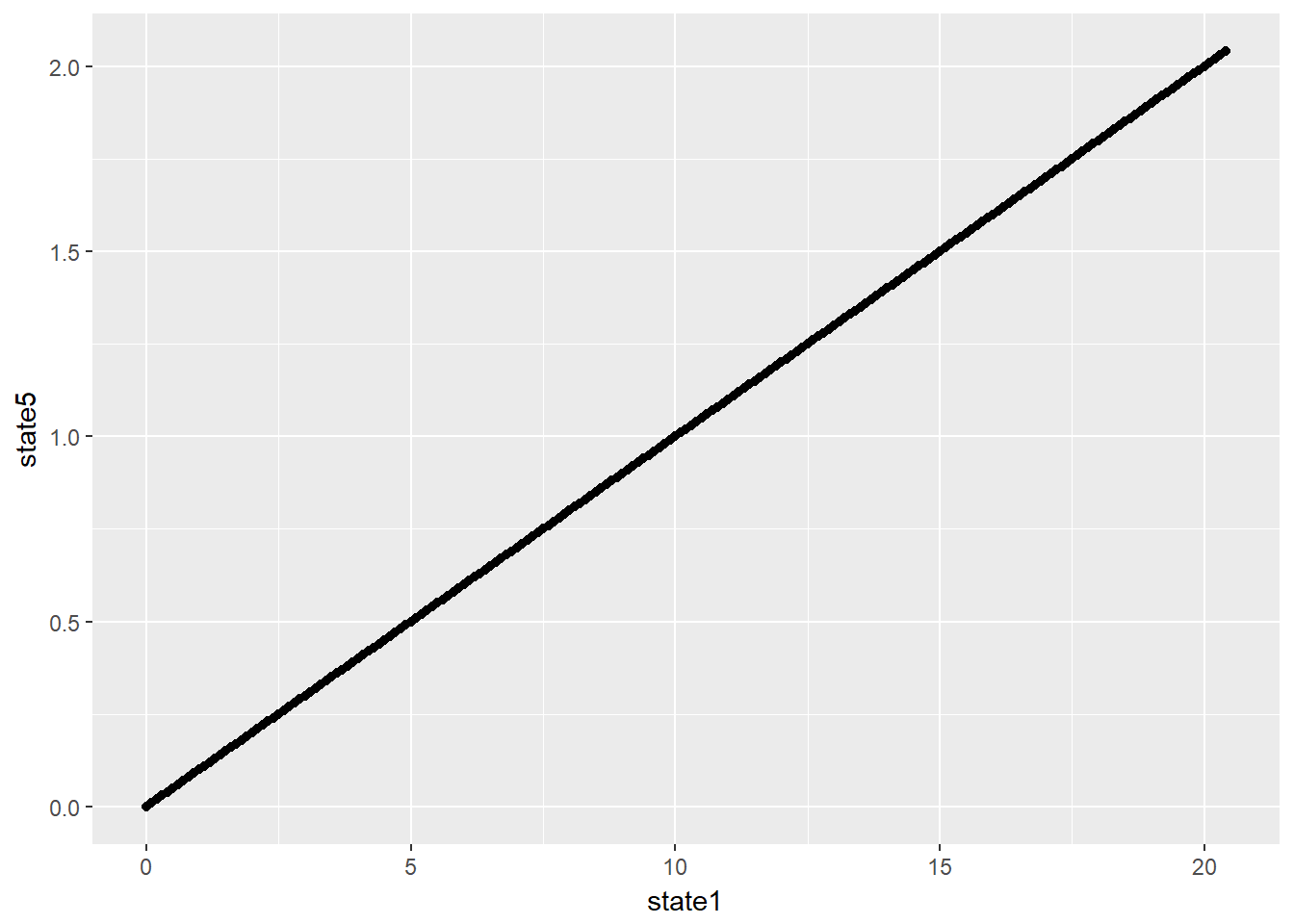
    print(qplot(state1, state5, data = datatable))
}

ProjectileApp()