Build the Reaction class with a RK4 solver

library(rODE)
# This code can also be found in the `examples` folder under this name:
# Reaction.R

# /**
# * Reaction models an autocatalytic oscillating chemical reaction
# * (Brusselator model) by implementing the ODE interface.
# * @author Wolfgang Christian
# * @version 1.0
# * Converted to R by: Alfonso R. Reyes
#
# */

setClass("Reaction", slots = c(
    k1 = "numeric",
    k2 = "numeric",
    k3 = "numeric",
    k4 = "numeric",
    A  = "numeric",
    B  = "numeric",
    state     = "numeric",
    odeSolver = "RK4"
    ),
    prototype = prototype(
        k1 = 1.0, k2 = 2.5, k3 = 1.0, k4 = 1.0,      # reaction rates
        A = 1, B = 1,                                # reactant concenterations
        state = c(0, 0, 0)      # X, Y, t
    ),
    contains = c("ODE")
    )

setMethod("getState", "Reaction", function(object) {
    object@state
})


setMethod("getRate", "Reaction", function(object, state, ...) {
    xxy <- state[1] * state[1] *state[2]
    object@rate[1] <- object@k1 * object@A - object@k2 * object@B * state[1] +
        object@k3 * xxy - object@k4 * state[1]                          # X rate
    object@rate[2] <- object@k2 * object@B * state[1] - object@k3 * xxy # Y rate
    object@rate[3] <- 1                         # rate of change of time, dt/dt
    object@rate                                 # time derivative
})

# constructor
Reaction <- function(initialConditions) {
    .Reaction <- new("Reaction")
    .Reaction@state <- initialConditions
    .Reaction
}

## [1] "getState"
## [1] "getRate"

Run the application ReactionApp

# +++++++++++++++++++++++++++++++++++++++++++++++++++ application: ReactionApp.R
# ReactionApp solves an autocatalytic oscillating chemical
# reaction (Brusselator model) using
# a fourth-order Runge-Kutta algorithm.

ReactionApp <- function(verbose = FALSE) {
    X <- 1; Y <- 5;
    dt <- 0.1
    reaction <- Reaction(c(X, Y, 0))
    solver  <- RK4(reaction)
    
    rowvec  <- vector("list")
    i <- 1
    while (getState(reaction)[3] < 100) {             # stop at t = 100
        rowvec[[i]] <- list(t = getState(reaction)[3],
                            X = getState(reaction)[1],
                            Y = getState(reaction)[2])
        solver   <- step(solver)
        reaction <- getODE(solver)
        i <-  i + 1
    }
    DT <- data.table::rbindlist(rowvec)
    return(DT)
}


solution <- ReactionApp()
plot(solution$t, solution$X)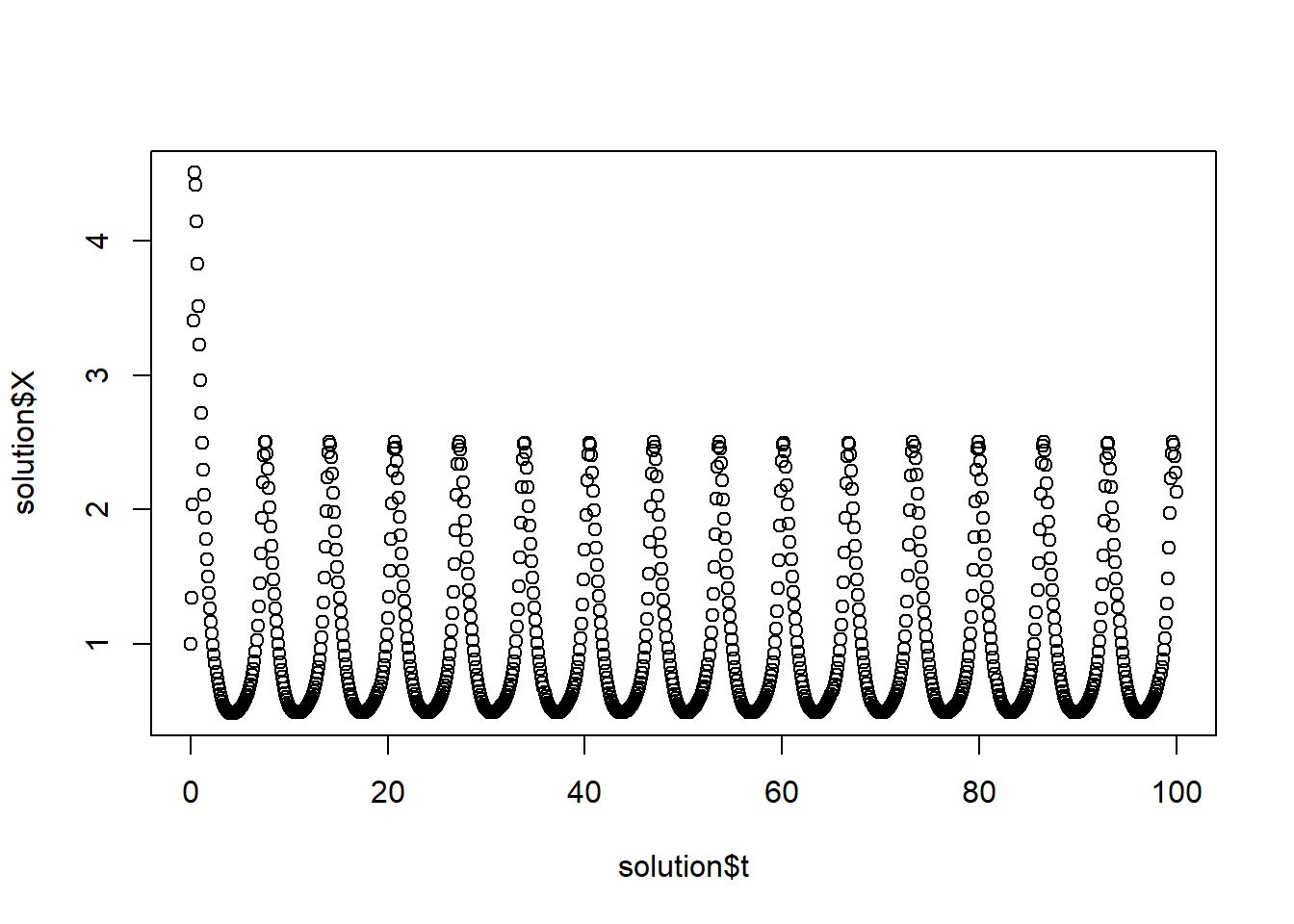

plot(solution$t, solution$Y)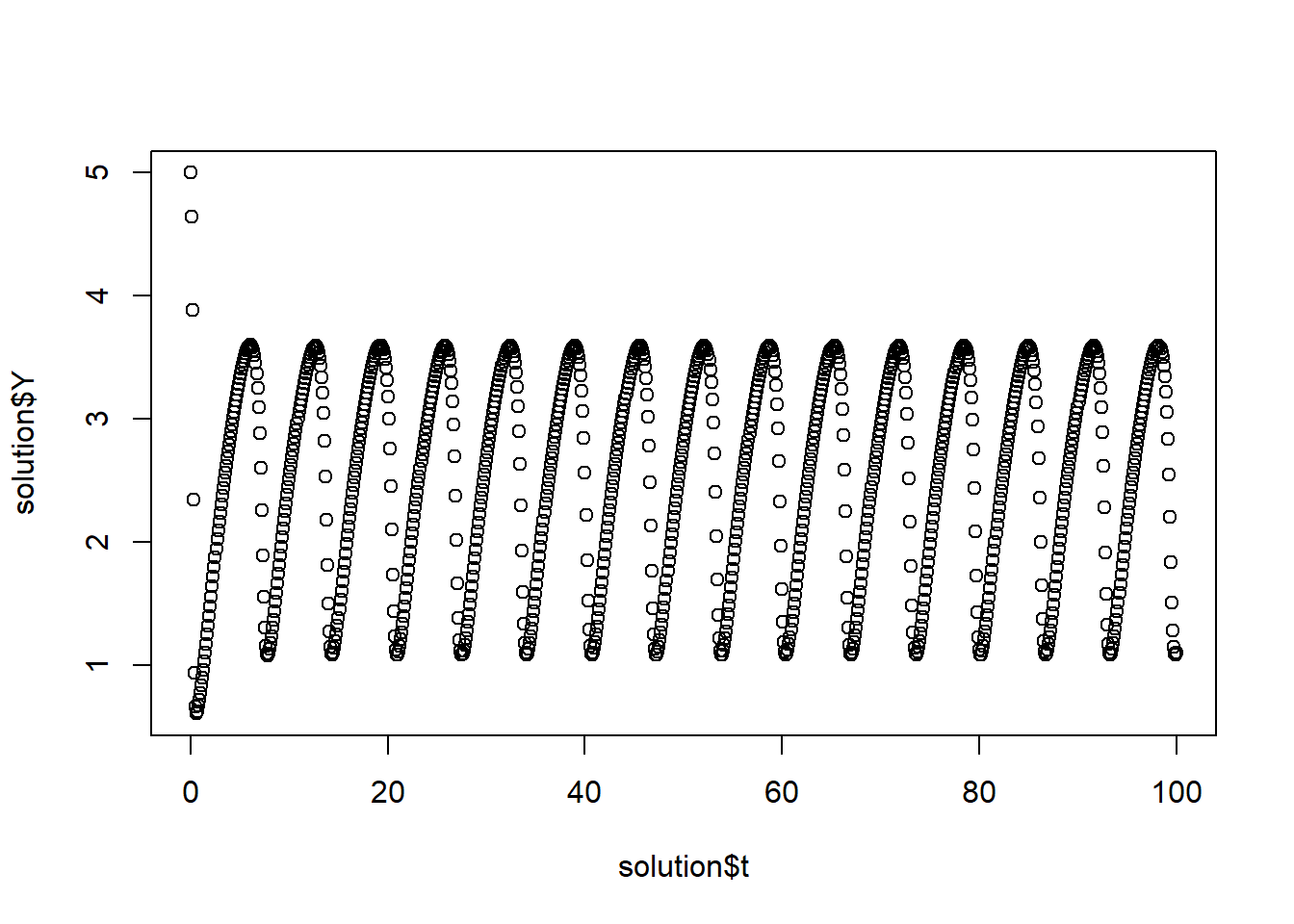

plot(solution$X, solution$Y)