The FallingParticleODE class using the Euler ODE solver

Because this is free fall of a particle in one-dimension, for vertical motion, we use Newton’s second law:

\[ m \frac{d^2y} {dt^2} = F \] and we know that the gravitational force is: \[ F = -mg \] Therefore: \[ m \frac{d^2y} {dt^2} = -g \] That expressing as first-order differential equations: \[ \frac {dy}{dt} = v \\ \frac {dv}{dt} = -g \]

(\(y\)), we define the numerical state equations as:

state[1]  x
state[2]  v
state[3]  t

From the equations of motion for a falling particle, the derivatives are: \[ \dot s_1 = s_2 \\ \dot s_2 = -g \\ \dot s_3 = 1 \] which is equivalent of writing this as the rate in the code: \[ r_1 = r_2 \\ r_2 = -g \\ r_3 = 1 \]

Build the FallingParticleODE class

We don’t indicate the ODE solver at this time. That is done in the application in the next section.

library(rODE)

# This code can also be found in the `examples` folder under this name:
# FallingParticleODE.R
#

setClass("FallingParticleODE", slots = c(
    g = "numeric"
    ),
    prototype = prototype(
        g = 9.8
    ),
    contains = c("ODE")
    )

setMethod("initialize", "FallingParticleODE", function(.Object, ...) {
    .Object@state <- vector("numeric", 3)
    return(.Object)
})

setMethod("getState", "FallingParticleODE", function(object, ...) {
    # Gets the state variables.
    return(object@state)
})

setMethod("getRate", "FallingParticleODE", function(object, state, ...) {
    # Gets the rate of change using the argument's state variables.
    object@rate[1] <- state[2]
    object@rate[2] <- - object@g
    object@rate[3] <- 1
    
    object@rate
})

# constructor
FallingParticleODE <- function(y, v) {
    .FallingParticleODE <- new("FallingParticleODE")
    .FallingParticleODE@state[1] <- y
    .FallingParticleODE@state[2] <- v
    .FallingParticleODE@state[3] <- 0
    .FallingParticleODE
}

## [1] "initialize"
## [1] "getState"
## [1] "getRate"

Run the application FallingParticleODEApp

# This code can also be found in the `examples` folder under this name:
# 
# FallingParticleODEApp.R
#
#
FallingParticleODEApp <- function(verbose = FALSE) {
    library(ggplot2)
    
    # load the R class that sets up the solver for this application
    
    initial_y <- 10   # initial y position
    initial_v <- 0    # initial x position
    dt        <- 0.01 # delta time for step
    
    
    ball <- FallingParticleODE(initial_y, initial_v)
    
    solver <- Euler(ball)
    solver <- setStepSize(solver, dt)
    
    rowVector <- vector("list")
    i <- 1
    # stop loop when the ball hits the ground
    while (ball@state[1] >= 0) {
        rowVector[[i]] <- list(state1 = ball@state[1], 
                               state2 = ball@state[2], 
                               state3 = ball@state[3])
        solver <- step(solver)
        ball <- solver@ode
        if (verbose) {
            cat(sprintf("%12f %12f ",  ball@state[1], ball@rate[1] ))
            cat(sprintf("%12f %12f ",  ball@state[2], ball@rate[2] ))
            cat(sprintf("%12f %12f\n", ball@state[3], ball@rate[3] ))
        }
        i <- i + 1
    }
    
    DT <- data.table::rbindlist(rowVector)
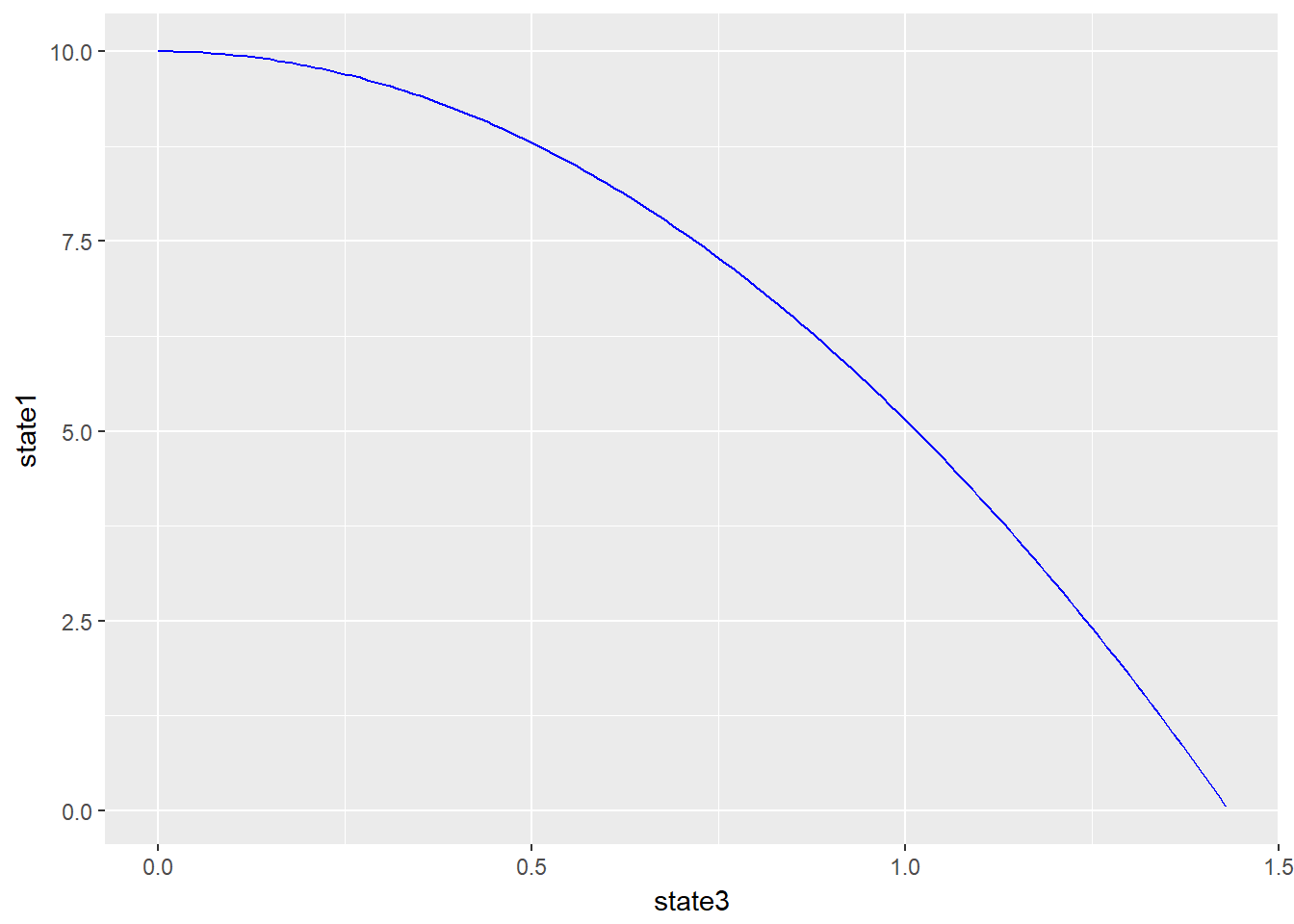
    print(ggplot(DT, aes(x = state3, y = state1)) + geom_line(col = "blue"))
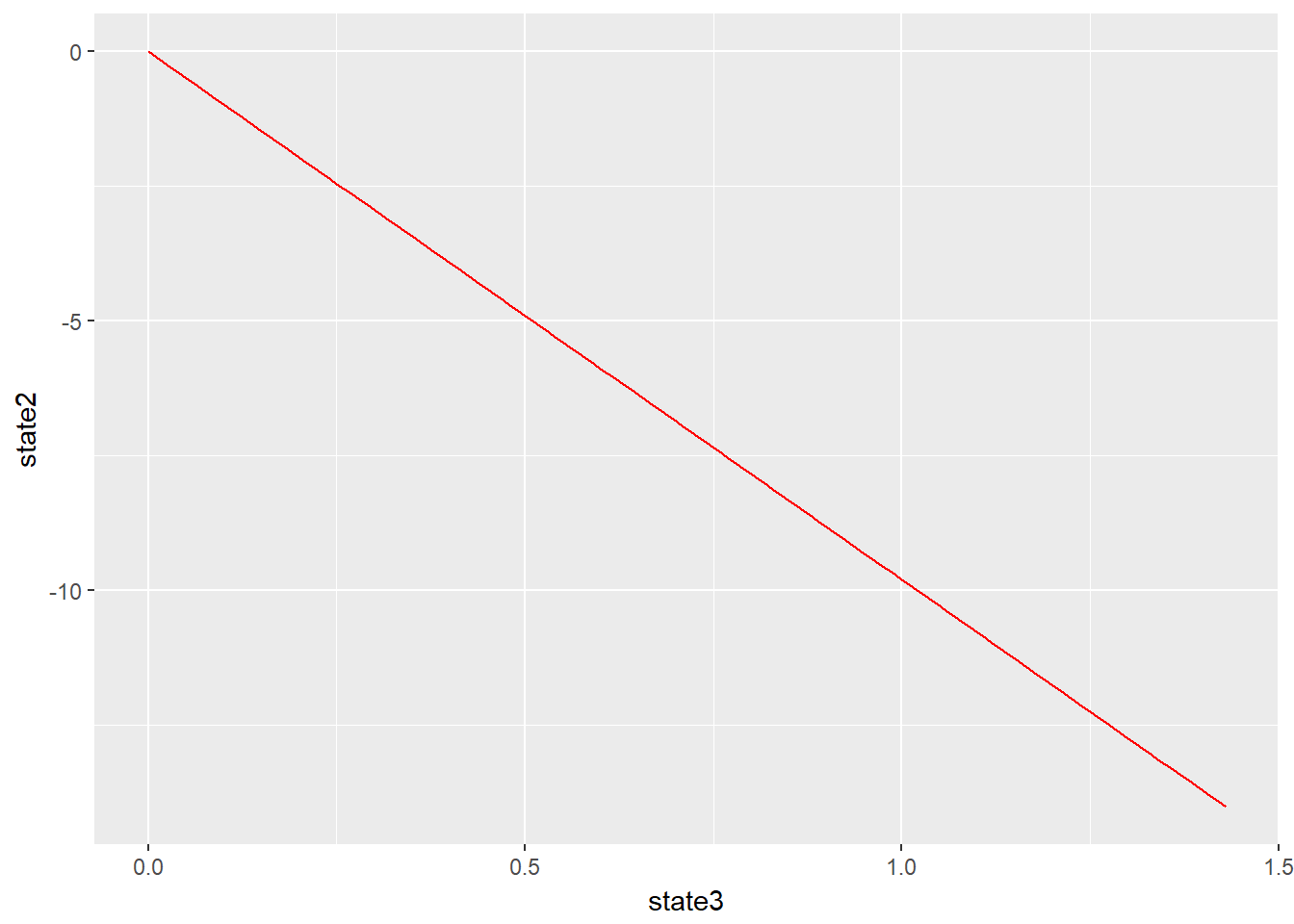
    print(ggplot(DT, aes(x = state3, y = state2)) + geom_line(col = "red"))
}


FallingParticleODEApp()