ODE class

Defines an ODE object for any solver

ODE constructor

ODE()

# S4 method for ODE
getState(object, ...)

# S4 method for ODE
getRate(object, state, ...)

Arguments

object	a class object
...	additional parameters
state	current state

Examples

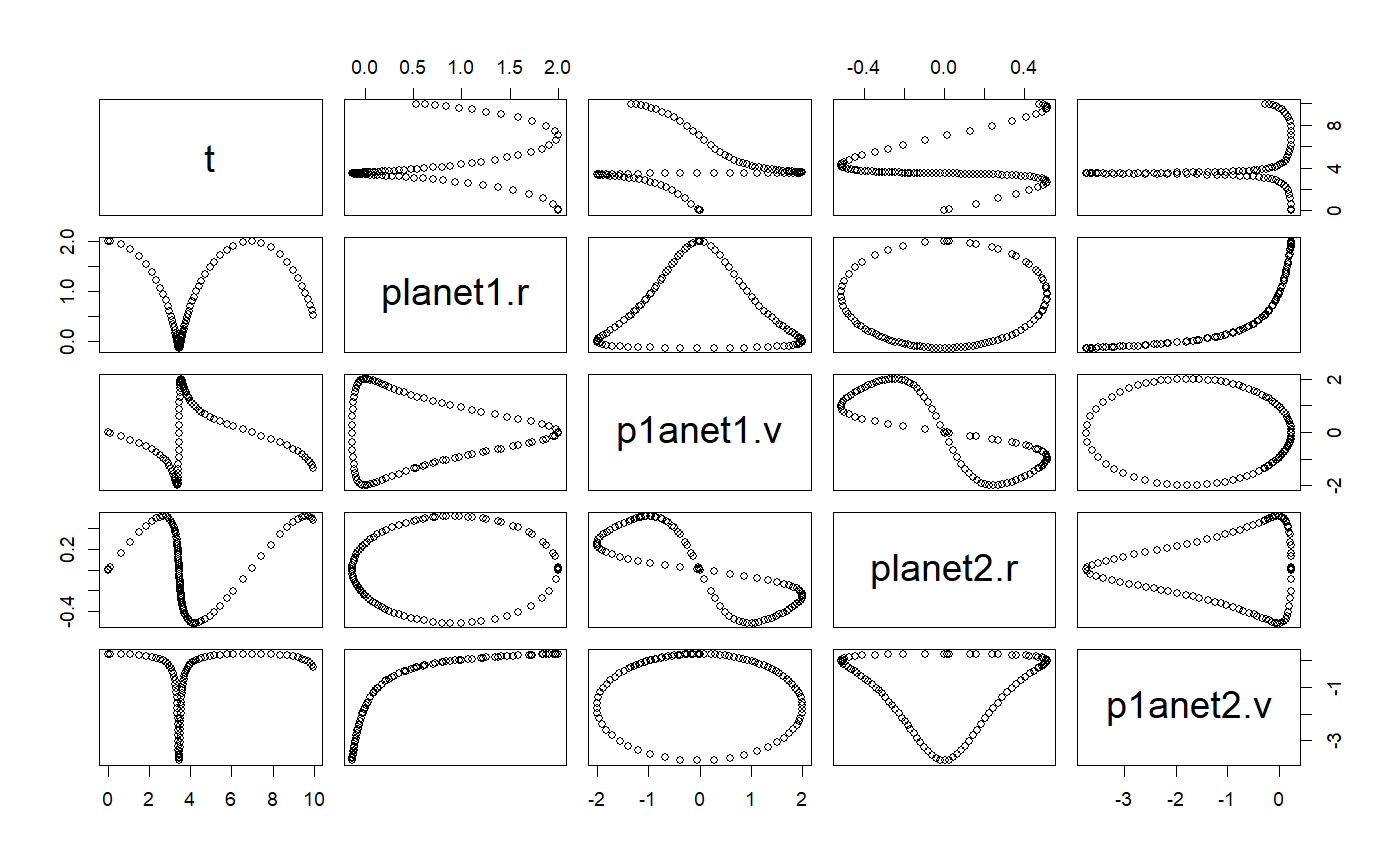
# ++++++++++++++++++++++++++++++++++++++++++++++++++      example: PendulumApp.R
# Simulation of a pendulum using the EulerRichardson ODE solver

suppressPackageStartupMessages(library(ggplot2))

importFromExamples("Pendulum.R")      # source the class

PendulumApp <- function(verbose = FALSE) {
    # initial values
    theta <- 0.2
    thetaDot <- 0
    dt <- 0.1
    pendulum <- Pendulum()
    # pendulum@state[3] <- 0      # set time to zero, t = 0
    pendulum <- setState(pendulum, theta, thetaDot)
    pendulum <- setStepSize(pendulum, dt = dt) # using stepSize in RK4
    pendulum@odeSolver <- setStepSize(pendulum@odeSolver, dt) # set new step size
    rowvec <- vector("list")
    i <- 1
    while (getState(pendulum)[3] <= 40)    {
        rowvec[[i]] <- list(t        = getState(pendulum)[3],    # time
                            theta    = getState(pendulum)[1], # angle
                            thetadot = getState(pendulum)[2]) # derivative of angle
        pendulum <- step(pendulum)
        i <- i + 1
    }
    DT <- data.table::rbindlist(rowvec)
    return(DT)
}
# show solution
solution <- PendulumApp()
plot(solution)
# +++++++++++++++++++++++++++++++++++++++++++++++++  example: PendulumEulerApp.R
# Pendulum simulation with the Euler ODE solver
# Notice how Euler is not applicable in this case as it diverges very quickly
# even when it is using a very small `delta t``?ODE

importFromExamples("PendulumEuler.R")      # source the class

PendulumEulerApp <- function(verbose = FALSE) {
    # initial values
    theta <- 0.2
    thetaDot <- 0
    dt <- 0.01
    pendulum <- PendulumEuler()
    pendulum@state[3] <- 0      # set time to zero, t = 0
    pendulum <- setState(pendulum, theta, thetaDot)
    stepSize <- dt
    pendulum <- setStepSize(pendulum, stepSize)
    pendulum@odeSolver <- setStepSize(pendulum@odeSolver, dt) # set new step size
    rowvec <- vector("list")
    i <- 1
    while (getState(pendulum)[3] <= 50)    {
        rowvec[[i]] <- list(t        = getState(pendulum)[3],
                            theta    = getState(pendulum)[1],
                            thetaDot = getState(pendulum)[2])
        pendulum <- step(pendulum)
        i <- i + 1
    }
    DT <- data.table::rbindlist(rowvec)
    return(DT)
}

solution <- PendulumEulerApp()
plot(solution)
#  +++++++++++++++++++++++++++++++++++++++++++++++++++++++++ example KeplerApp.R
#  KeplerApp solves an inverse-square law model (Kepler model) using an adaptive
#  stepsize algorithm.
#  Application showing two planet orbiting
#  File in examples: KeplerApp.R

importFromExamples("Kepler.R") # source the class Kepler

KeplerApp <- function(verbose = FALSE) {

    # set the orbit into a predefined state.
    r <- c(2, 0)                                   # orbit radius
    v <- c(0, 0.25)                                # velocity
    dt <- 0.1
    planet <- Kepler(r, v)                         # make up an ODE object
    solver <- RK45(planet)
    rowVector <- vector("list")
    i <- 1
    while (getState(planet)[5] <= 10) {
        rowVector[[i]] <- list(t  = planet@state[5],
                               planet1.r = getState(planet)[1],
                               p1anet1.v = getState(planet)[2],
                               planet2.r = getState(planet)[3],
                               p1anet2.v = getState(planet)[4])
        solver <- step(solver)
        planet <- getODE(solver)
        i <-  i + 1
    }
    DT <- data.table::rbindlist(rowVector)

    return(DT)
}

solution <- KeplerApp()
plot(solution)


# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ base class: FallingParticleODE.R
# Class definition for application FallingParticleODEApp.R

setClass("FallingParticleODE", slots = c(
        g = "numeric"
        ),
        prototype = prototype(
            g = 9.8
        ),
        contains = c("ODE")
        )


setMethod("initialize", "FallingParticleODE", function(.Object, ...) {
    .Object@state <- vector("numeric", 3)
    return(.Object)
})
#> [1] "initialize"

setMethod("getState", "FallingParticleODE", function(object, ...) {
    # Gets the state variables.
    return(object@state)
})
#> [1] "getState"

setMethod("getRate", "FallingParticleODE", function(object, state, ...) {
    # Gets the rate of change using the argument's state variables.
    object@rate[1] <- state[2]
    object@rate[2] <- - object@g
    object@rate[3] <- 1

    object@rate
})
#> [1] "getRate"

# constructor
FallingParticleODE <- function(y, v) {
    .FallingParticleODE <- new("FallingParticleODE")
    .FallingParticleODE@state[1] <- y
    .FallingParticleODE@state[2] <- v
    .FallingParticleODE@state[3] <- 0
    .FallingParticleODE
}