7 Visualizing distributions: Histograms and density plots
We frequently encounter the situation where we would like to understand how a particular variable is distributed in a dataset. To give a concrete example, we will consider the passengers of the Titanic, a data set we encountered already in Chapter 6. There were approximately 1300 passengers on the Titanic (not counting crew), and we have reported ages for 756 of them. We might want to know how many passengers of what ages there were on the Titanic, i.e., how many children, young adults, middle-aged people, seniors, and so on. We call the relative proportions of different ages among the passengers the age distribution of the passengers.
7.1 Visualizing a single distribution
We can obtain a sense of the age distribution among the passengers by grouping all passengers into bins with comparable ages and then counting the number of passengers in each bin. This procedure results in a table such as Table 7.1.
|
|
|
We can visualize this table by drawing filled rectangles whose heights correspond to the counts and whose widths correspond to the width of the age bins (Figure 7.1). Such a visualization is called a histogram. (Note that all bins must have the same width for the visualization to be a valid histogram.)

Figure 7.1: Histogram of the ages of Titanic passengers.
Because histograms are generated by binning the data, their exact visual appearance depends on the choice of the bin width. Most visualization programs that generate histograms will choose a bin width by default, but chances are that bin width is not the most appropriate one for any histogram you may want to make. It is therefore critical to always try different bin widths to verify that the resulting histogram reflects the underlying data accurately. In general, if the bin width is too small, then the histogram becomes overly peaky and visually busy and the main trends in the data may be obscured. On the other hand, if the bin width is too large, then smaller features in the distribution of the data, such as the dip around age 10, may disappear.
For the age distribution of Titanic passengers, we can see that a bin width of one year is too small and a bin width of fifteen years is too large, whereas bin widths between three to five years work fine (Figure 7.2).
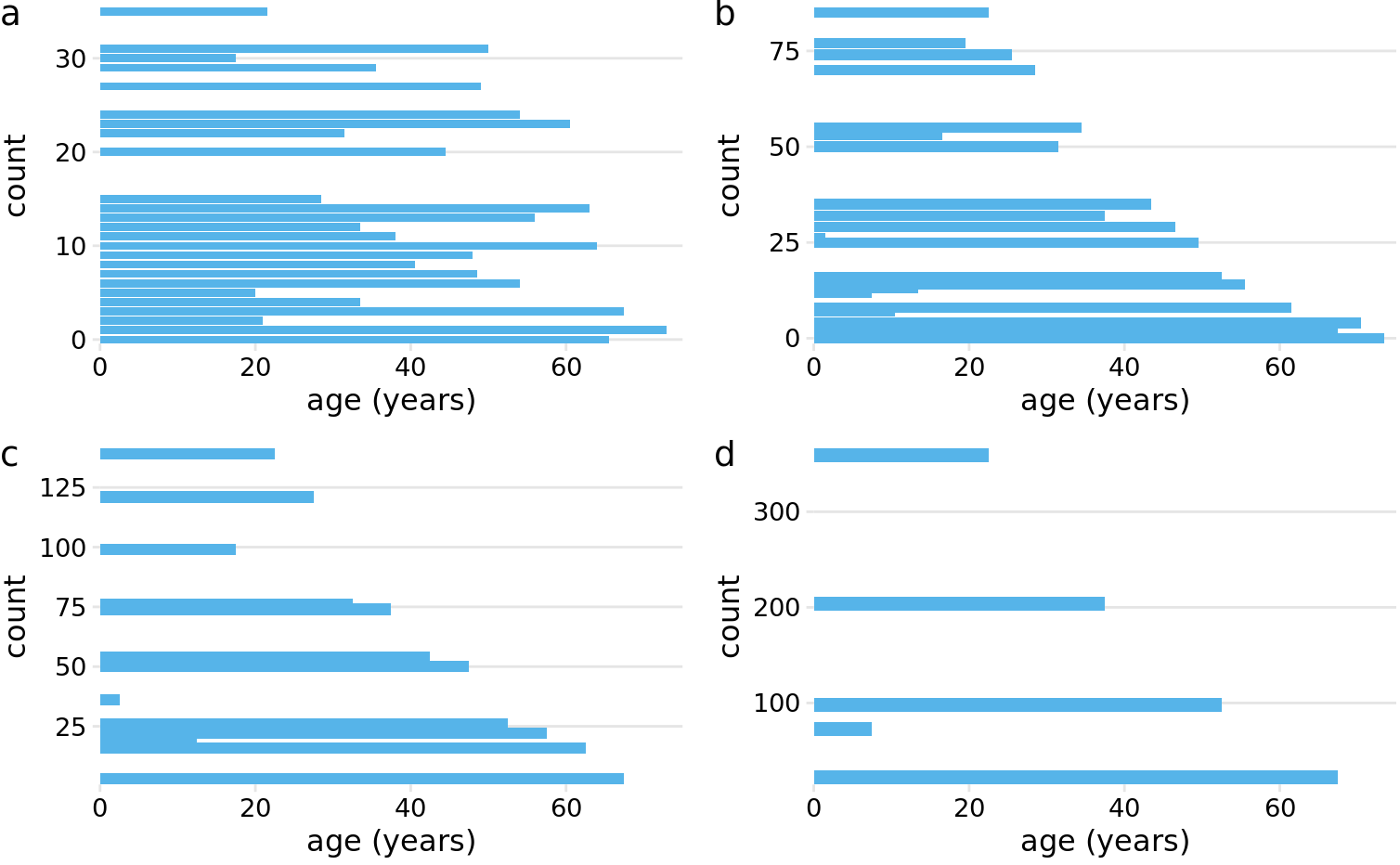
Figure 7.2: Histograms depend on the chosen bin width. Here, the same age distribution of Titanic passengers is shown with four different bin widths: (a) one year; (b) three years; (c) five years; (d) fifteen years.
When making a histogram, always explore multiple bin widths.
Histograms have been a popular visualization option since at least the 18th century, in part because they are easily generated by hand. More recently, as extensive computing power has become available in everyday devices such as laptops and cell phones, we see them increasingly being replaced by density plots. In a density plot, we attempt to visualize the underlying probability distribution of the data by drawing an appropriate continuous curve (Figure 7.3). This curve needs to be estimated from the data, and the most commonly used method for this estimation procedure is called kernel density estimation. In kernel density estimation, we draw a continuous curve (the kernel) with a small width (controlled by a parameter called bandwidth) at the location of each data point, and then we add up all these curves to obtain the final density estimate. The most widely used kernel is a Gaussian kernel (i.e., a Gaussian bell curve), but there are many other choices.
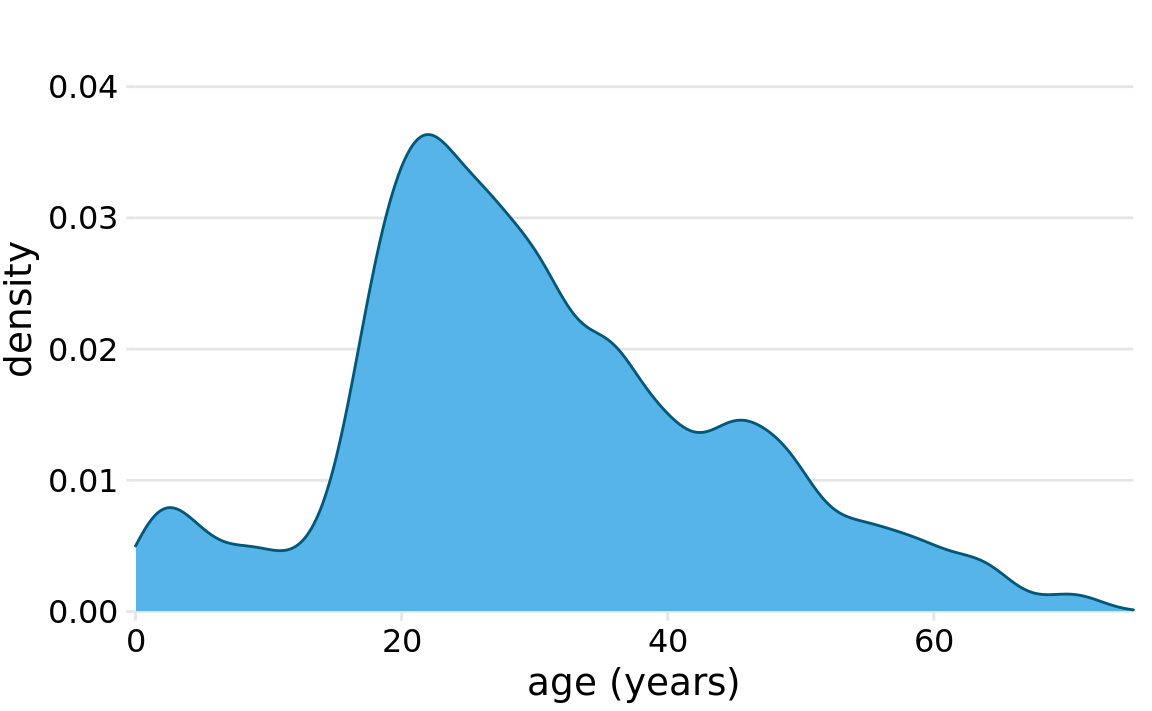
Figure 7.3: Kernel density estimate of the age distribution of passengers on the Titanic. The height of the curve is scaled such that the area under the curve equals one. The density estimate was performed with a Gaussian kernel and a bandwidth of 2.
Just as is the case with histograms, the exact visual appearance of a density plot depends on the kernel and bandwidth choices (Figure 7.4). The bandwidth parameter behaves similarly to the bin width in histograms. If the bandwidth is too small, then the density estimate can become overly peaky and visually busy and the main trends in the data may be obscured. On the other hand, if the bandwidth is too large, then smaller features in the distribution of the data may disappear. In addition, the choice of the kernel affects the shape of the density curve. For example, a Gaussian kernel will have a tendency to produce density estimates that look Gaussian-like, with smooth features and tails. By contrast, a rectangular kernel can generate the appearance of steps in the density curve (Figure 7.4d). In general, the more data points there are in the data set, the less the choice of the kernel matters. Therefore, density plots tend to be quite reliable and informative for large data sets but can be misleading for data sets of only a few points.
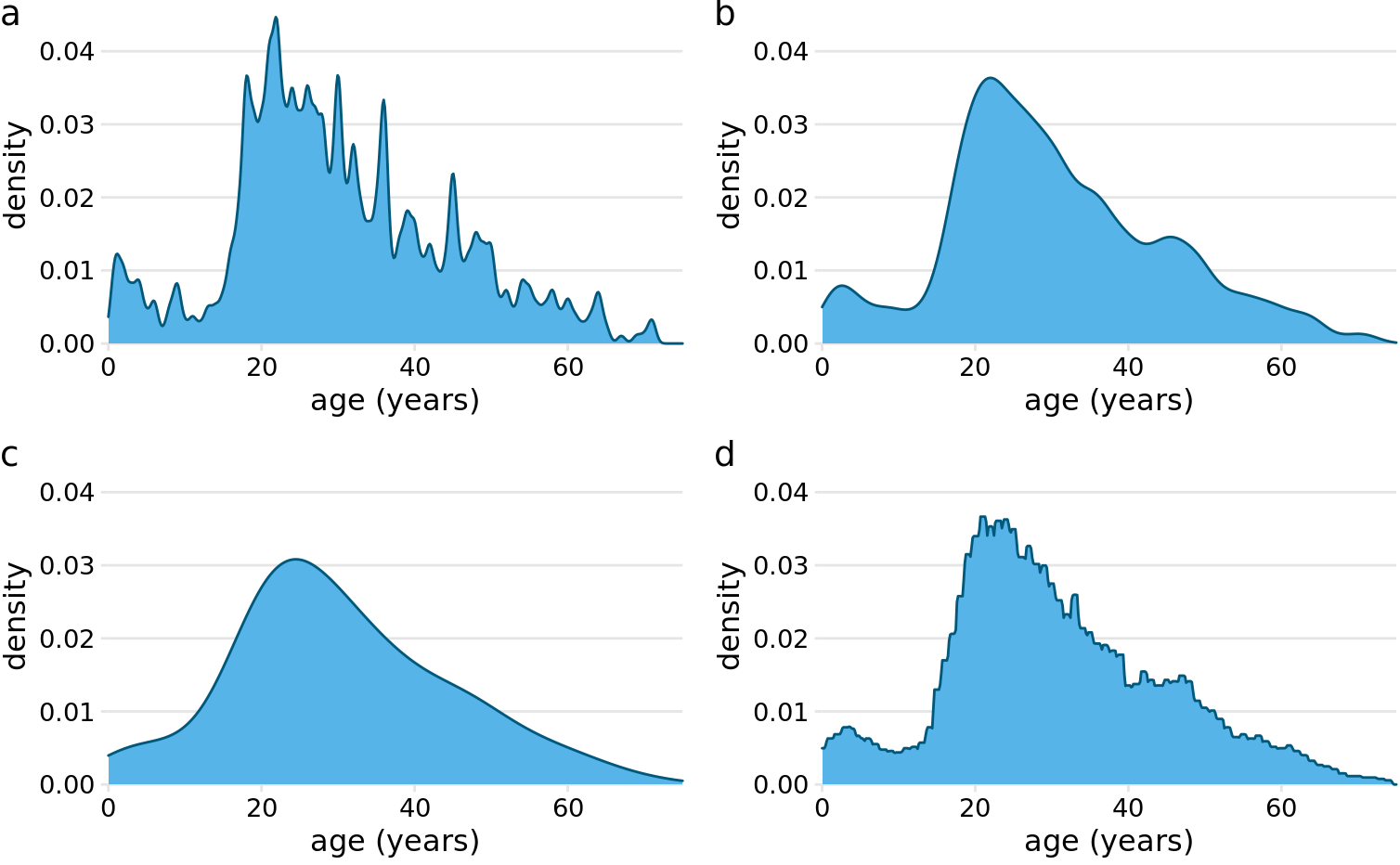
Figure 7.4: Kernel density estimates depend on the chosen kernel and bandwidth. Here, the same age distribution of Titanic passengers is shown for four different combinations of these parameters: (a) Gaussian kernel, bandwidth = 0.5; (b) Gaussian kernel, bandwidth = 2; (c) Gaussian kernel, bandwidth = 5; (d) Rectangular kernel, bandwidth = 2.
Density curves are usually scaled such that the area under the curve equals one. This convention can make the y axis scale confusing, because it depends on the units of the x axis. For example, in the case of the age distribution, the data range on the x axis goes from 0 to approximately 75. Therefore, we expect the mean height of the density curve to be 1/75 = 0.013. Indeed, when looking at the age density curves (e.g., Figure 7.4), we see that the y values range from 0 to approximately 0.04, with an average of somewhere close to 0.01.
Kernel density estimates have one pitfall that we need to be aware of: They have a tendency to produce the appearance of data where none exists, in particular in the tails. As a consequence, careless use of density estimates can easily lead to figures that make nonsensical statements. For example, if we don’t pay attention, we might generate a visualization of an age distribution that includes negative ages (Figure 7.5).

Figure 7.5: Kernel density estimates can extend the tails of the distribution into areas where no data exist and no data are even possible. Here, the density estimate has been allowed to extend into the negative age range. This is clearly nonsensical and should be avoided.
Always verify that your density estimate does not predict the existence of nonsensical data values.
So should you use a histogram or a density plot to visualize a distribution? Heated discussions can be had on this topic. Some people are vehemently against density plots and believe that they are arbitrary and misleading. Others realize that histograms can be just as arbitrary and misleading. I think the choice is largely a matter of taste, but sometimes one or the other option may more accurately reflect the specific features of interest in the data at hand. There is also the possibility of using neither and instead choosing empirical cumulative density functions or q-q plots (Chapter 8). Finally, I believe that density estimates have an inherent advantage over histograms as soon as we want to visualize more than one distribution at a time (see next section).
7.2 Visualizing multiple distributions at the same time
In many scenarios we have multiple distributions we would like to visualize simultaneously. For example, let’s say we’d like to see how the ages of Titanic passengers are distributed between men and women. Were men and women passengers generally of the same age, or was there an age difference between the genders? One commonly employed visualization strategy in this case is a stacked histogram, where we draw the histogram bars for women on top of the bars for men, in a different color (Figure 7.6).
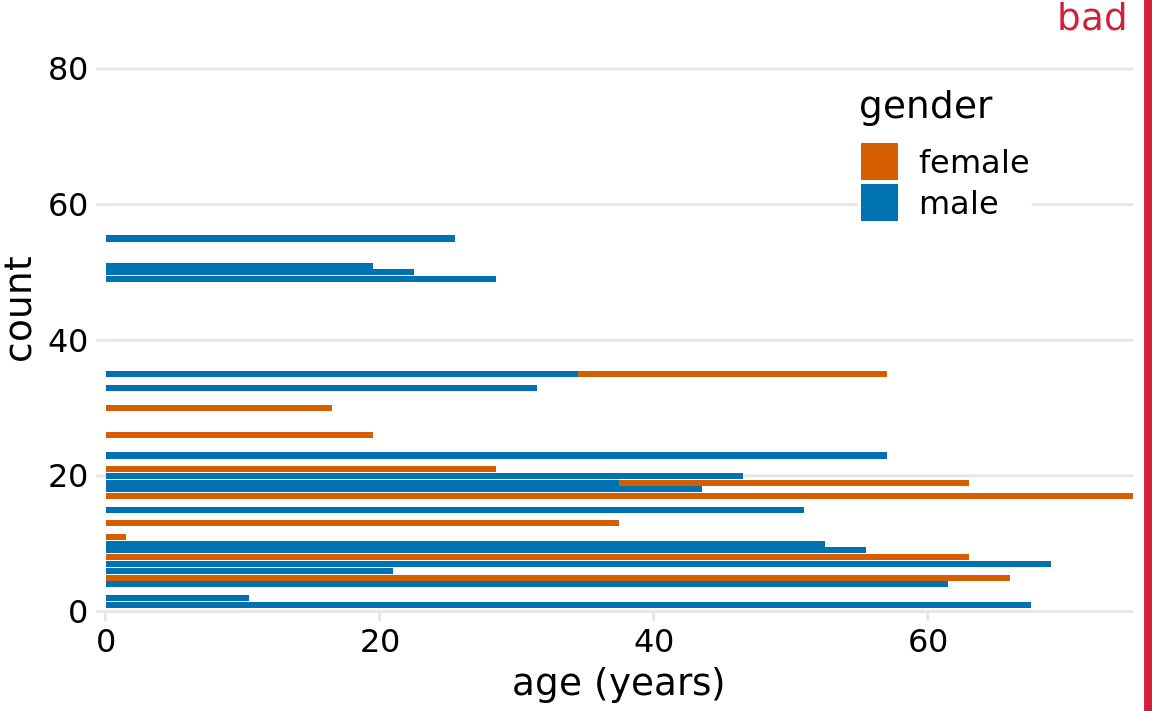
Figure 7.6: Histogram of the ages of Titanic passengers stratified by gender. This figure has been labeled as “bad” because stacked histograms are easily confused with overlapping histograms (see also Figure 7.7). In addition, the heights of the bars representing female passengers cannot easily be compared to each other.
In my opinion, this type of visualization should be avoided. There are two key problems here: First, from just looking at the figure, it is never entirely clear where exactly the bars begin. Do they start where the color changes or are they meant to start at zero? In other words, are there about 25 females of age 18–20 or are there almost 80? (The former is the case.) Second, the bar heights for the female counts cannot be directly compared to each other, because the bars all start at a different height. For example, the men were on average older than the women, and this fact is not at all visible in Figure 7.6.
We could try to address these problems by having all bars start at zero and making the bars partially transparent (Figure 7.7).
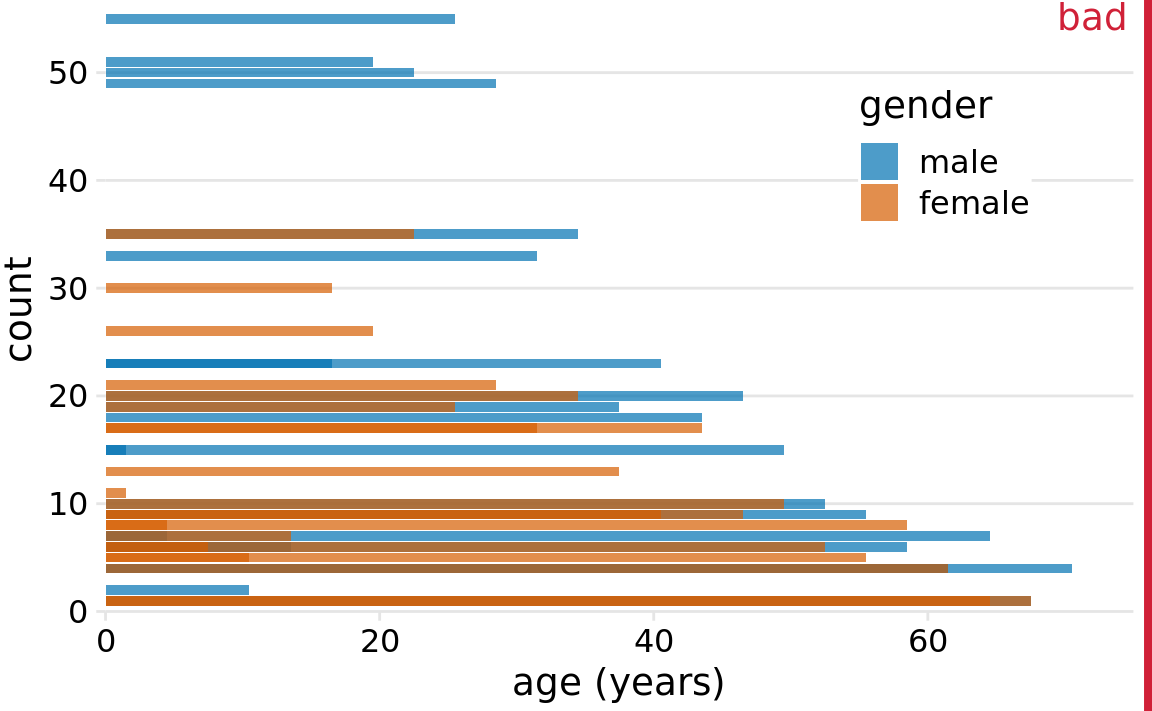
Figure 7.7: Age distributions of male and female Titanic passengers, shown as two overlapping histograms. This figure has been labeled as “bad” because there is no clear visual indication that all blue bars start at a count of 0.
However, this approach generates new problems. Now it appears that there are actually three different groups, not just two, and we’re still not entirely sure where each bar starts and ends. Overlapping histograms don’t work well because a semi-transparent bar drawn on top of another tends to not look like a semi-transparent bar but instead like a bar drawn in a different color.
Overlapping density plots don’t typically have the problem that overlapping histograms have, because the continuous density lines help the eye keep the distributions separate. However, for this particular dataset, the age distributions for male and female passengers are nearly identical up to around age 17 and then diverge, so that the resulting visualization is still not ideal (Figure 7.8).
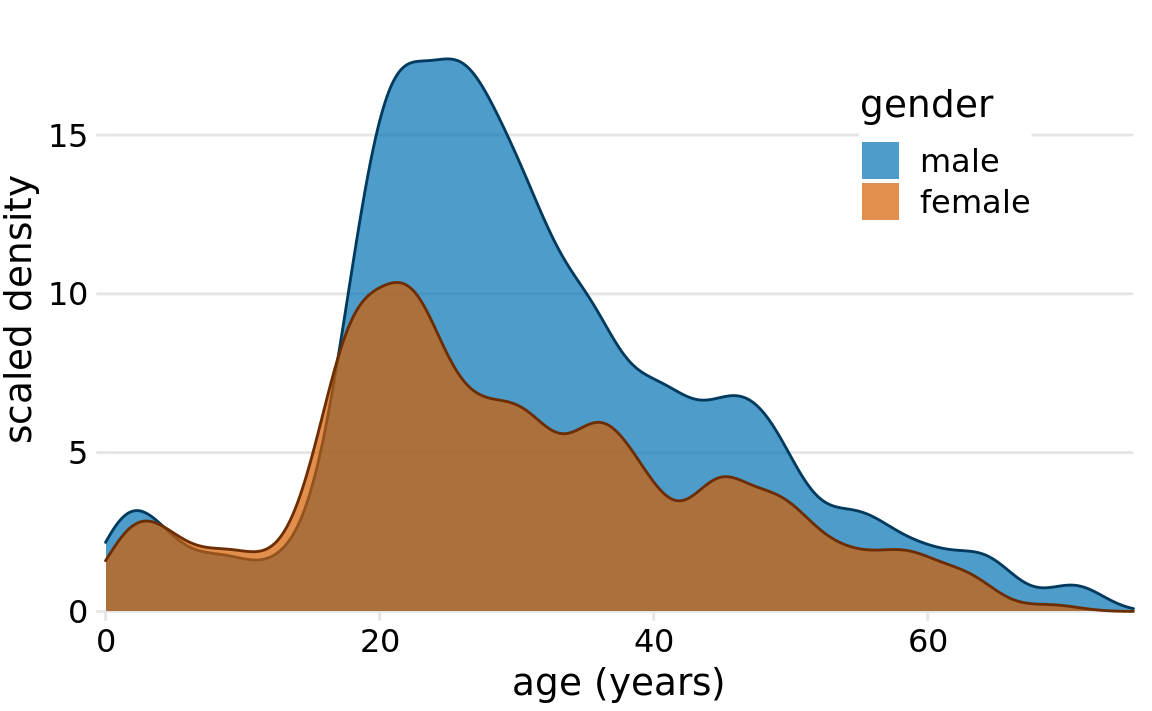
Figure 7.8: Density estimates of the ages of male and female Titanic passengers. To highlight that there were more male than female passengers, the density curves were scaled such that the area under each curve corresponds to the total number of male and female passengers with known age (468 and 288, respectively).
A solution that works well for this dataset is to show the age distributions of male and female passengers separately, each as a proportion of the overall age distribution (Figure 7.9). This visualization shows intuitively and clearly that there were many fewer women than men in the 20–50-year age range on the Titanic.
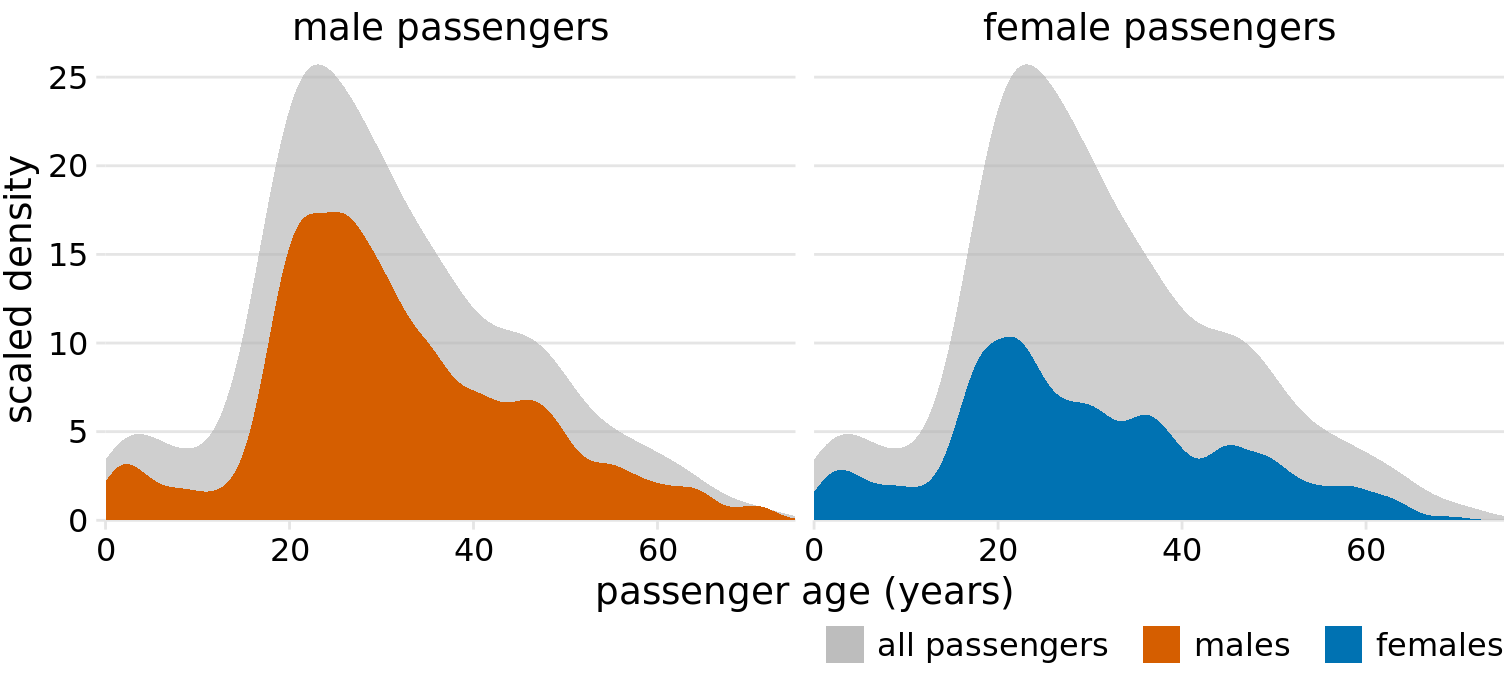
Figure 7.9: Age distributions of male and female Titanic passengers, shown as proportion of the passenger total. The colored areas show the density estimates of the ages of male and female passengers, respectively, and the gray areas show the overall passenger age distribution.
Finally, when we want to visualize exactly two distributions, we can also make two separate histograms, rotate them by 90 degrees, and have the bars in one histogram point into the opposite direction of the other. This trick is commonly employed when visualizing age distributions, and the resulting plot is usually called an age pyramid (Figure 7.10).
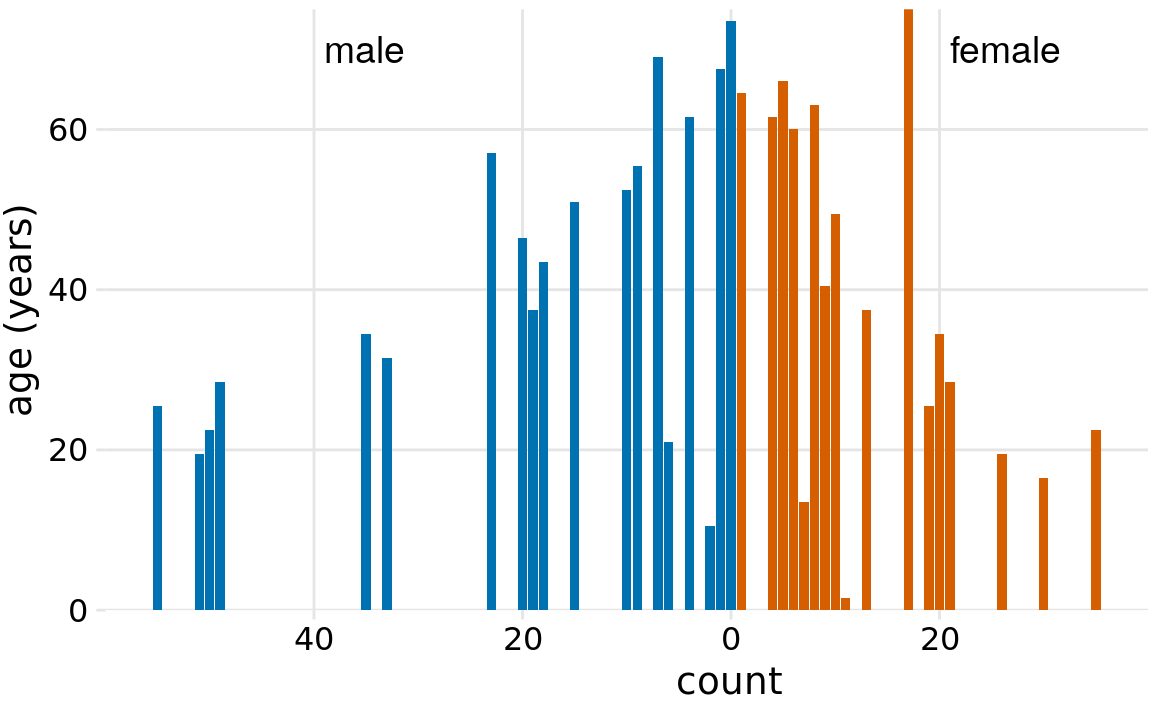
Figure 7.10: The age distributions of male and female Titanic passengers visualized as an age pyramid.
Importantly, this trick does not work when there are more than two distributions we want to visualize at the same time. For multiple distributions, histograms tend to become highly confusing, whereas density plots work well as long as the distributions are somewhat distinct and contiguous. For example, to visualize the distribution of butterfat percentage among cows from four different cattle breeds, density plots are fine (Figure 7.11).
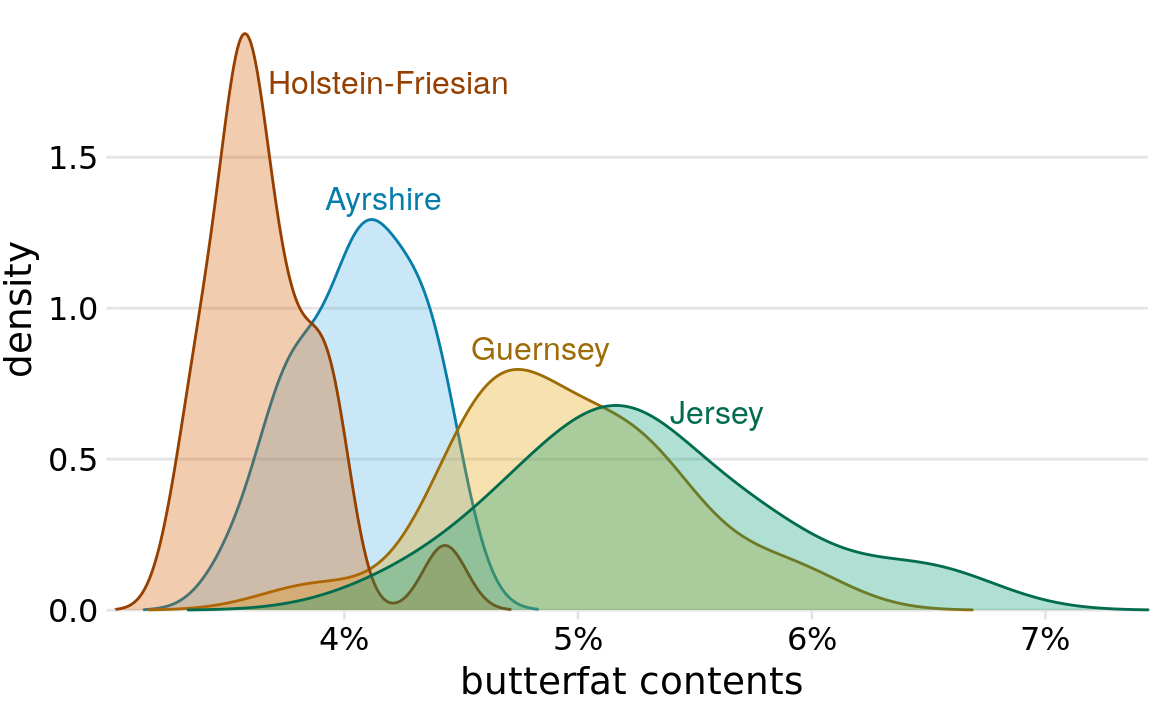
Figure 7.11: Density estimates of the butterfat percentage in the milk of four cattle breeds. Data Source: Canadian Record of Performance for Purebred Dairy Cattle
To visualize several distributions at once, kernel density plots will generally work better than histograms.