13 Visualizing time series and other functions of an independent variable

The preceding chapter discussed scatter plots, where we plot one quantitative variable against another. A special case arises when one of the two variables can be thought of as time, because time imposes additional structure on the data. Now the data points have an inherent order; we can arrange the points in order of increasing time and define a predecessor and successor for each data point. We frequently want to visualize this temporal order and we do so with line graphs. Line graphs are not limited to time series, however. They are appropriate whenever one variable imposes an ordering on the data. This scenario arises also, for example, in a controlled experiment where a treatment variable is purposefully set to a range of different values. If we have multiple variables that depend on time, we can either draw separate line plots or we can draw a regular scatter plot and then draw lines to connect the neighboring points in time.

13.1 Individual time series

As a first demonstration of a time series, we will consider the pattern of monthly preprint submissions in biology. Preprints are scientific articles that researchers post online before formal peer review and publication in a scientific journal. The preprint server bioRxiv, which was founded in November 2013 specifically for researchers working in the biological sciences, has seen substantial growth in monthly submissions since. We can visualize this growth by making a form of scatter plot (Chapter 12) where we draw dots representing the number of submissions in each month (Figure 13.1).

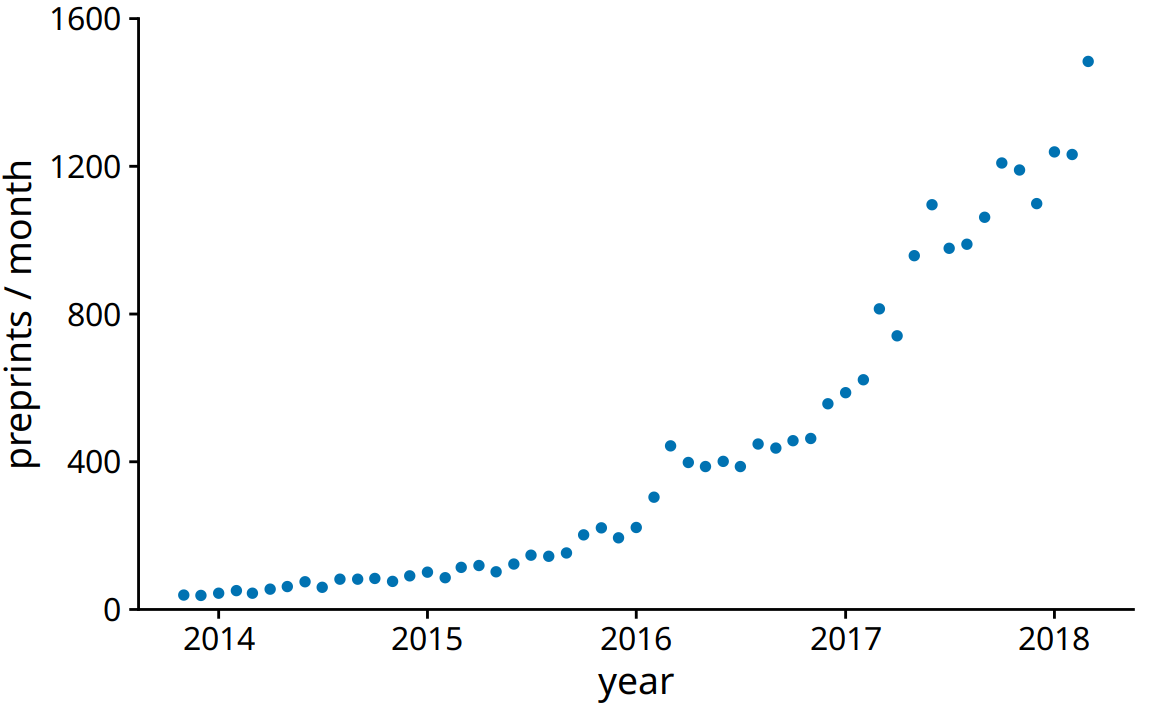
Figure 13.1: Monthly submissions to the preprint server bioRxiv, from its inception in November 2014 until April 2018. Each dot represents the number of submissions in one month. There has been a steady increase in submission volume throughout the entire 4.5-year period. Data source: Jordan Anaya, http://www.prepubmed.org/

There is an important difference however between Figure 13.1 and the scatter plots discussed in Chapter 12. In Figure 13.1, the dots are spaced evenly along the x axis, and there is a defined order among them. Each dot has exactly one left and one right neighbor (except the leftmost and rightmost points which have only one neighbor each). We can visually emphasize this order by connecting neighboring points with lines (Figure 13.2). Such a plot is called a line graph.

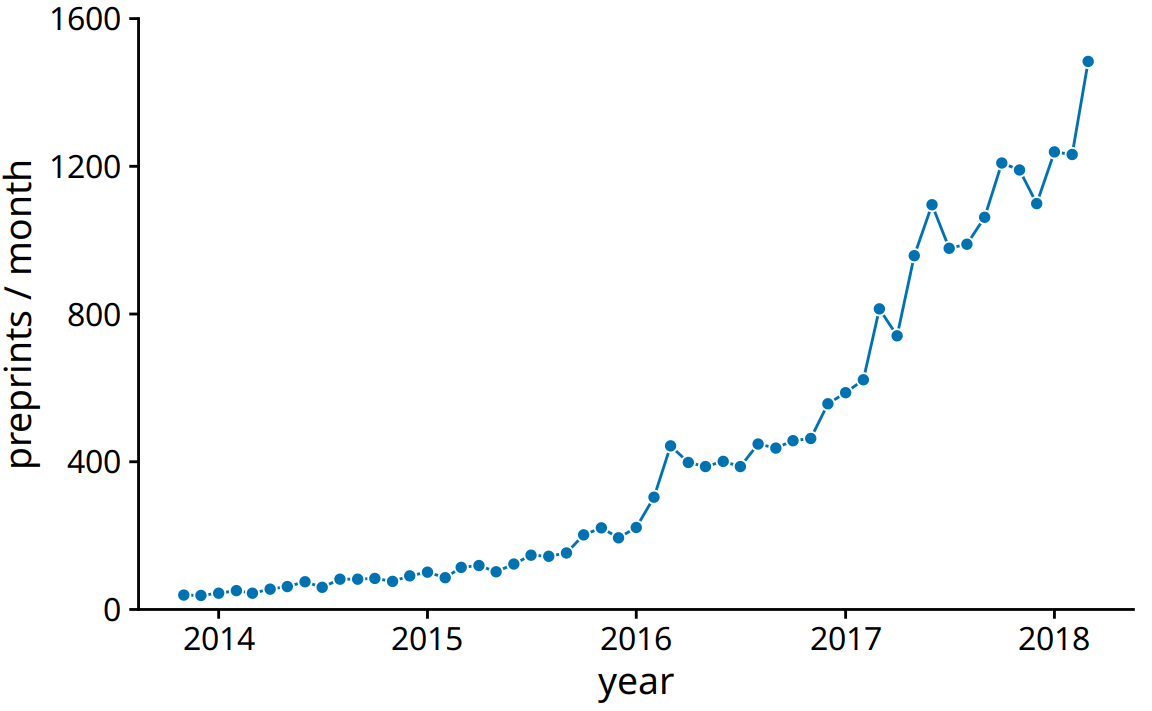
Figure 13.2: Monthly submissions to the preprint server bioRxiv, shown as dots connected by lines. The lines do not represent data but are only meant as a guide to the eye. By connecting the individual dots with lines, we emphasize that there is an order between the dots, each dot has exactly one neighbor that comes before and one that comes after. Data source: Jordan Anaya, http://www.prepubmed.org/

Some people object to drawing lines between points because the lines do not represent observed data. In particular, if there are only a few observations spaced far apart, had observations been made at intermediate times they would probably not have fallen exactly onto the lines shown. Thus, in a sense, the lines correspond to made-up data. Yet they may help with perception when the points are spaced far apart or are unevenly spaced. We can somewhat resolve this dilemma by pointing it out in the figure caption, for example by writing “lines are meant as a guide to the eye” (see caption of Figure 13.2).

Using lines to represent time series is generally accepted practice, however, and frequently the dots are omitted altogether (Figure 13.3). Without dots, the figure places more emphasis on the overall trend in the data and less on individual observations. A figure without dots is also visually less busy. In general, the denser the time series, the less important it is to show individual obserations with dots. For the preprint dataset shown here, I think omitting the dots is fine.

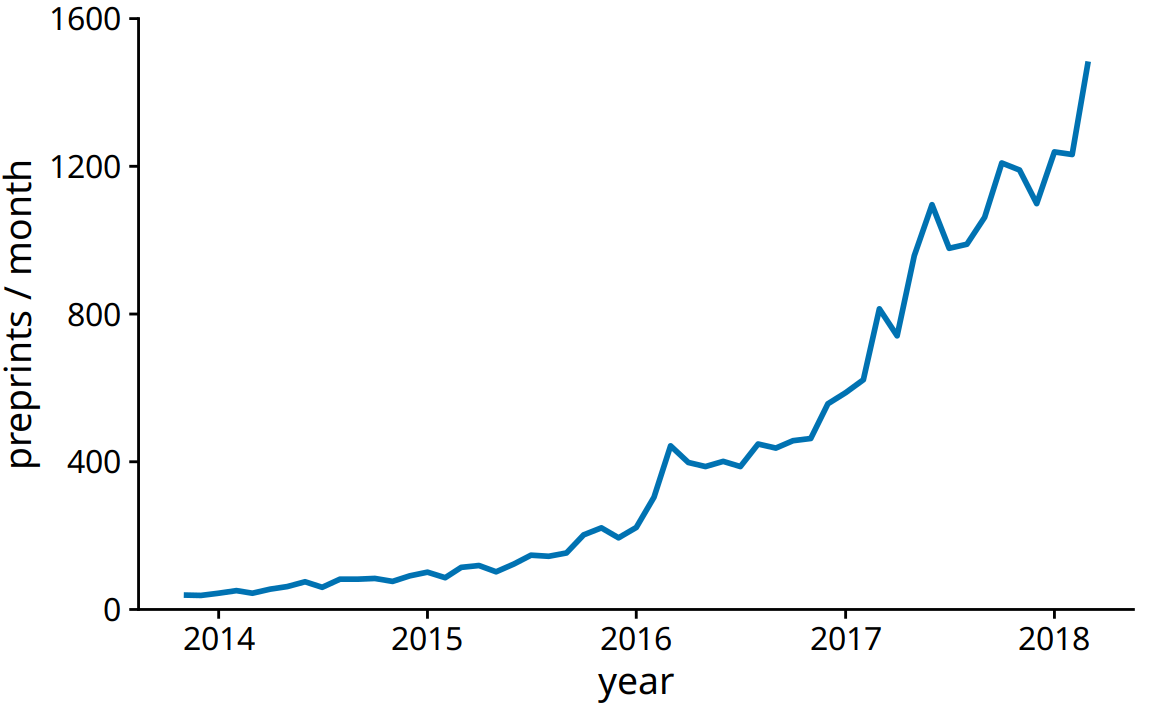
Figure 13.3: Monthly submissions to the preprint server bioRxiv, shown as a line graph without dots. Omitting the dots emphasizes the overall temporal trend while de-emphasizing individual observations at specific time points. It is particularly useful when the time points are spaced very densely. Data source: Jordan Anaya, http://www.prepubmed.org/

We can also fill the area under the curve with a solid color (Figure 13.4). This choice further emphasizes the overarching trend in the data, because it visually separates the area above the curve from the area below. However, this visualization is only valid if the y axis starts at zero, so that the height of the shaded area at each time point represents the data value at that time point.

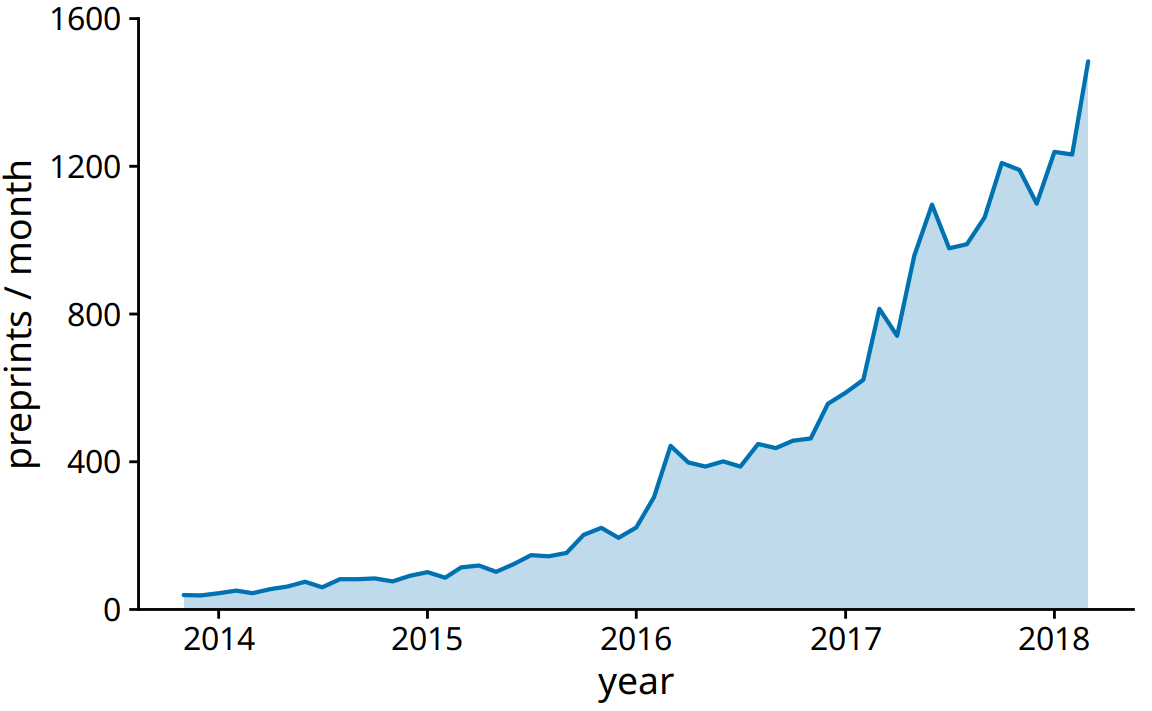
Figure 13.4: Monthly submissions to the preprint server bioRxiv, shown as a line graph with filled area underneath. By filling the area under the curve, we put even more emphasis on the overarching temporal trend than if we just draw a line (Figure 13.3). Data source: Jordan Anaya, http://www.prepubmed.org/

13.2 Multiple time series and dose–response curves

We often have multiple time courses that we want to show at once. In this case, we have to be more careful in how we plot the data, because the figure can become confusing or difficult to read. For example, if we want to show the monthly submissions to multiple preprint servers, a scatter plot is not a good idea, because the individual time courses run into each other (Figure 13.5). Connecting the dots with lines alleviates this issue (Figure 13.6).

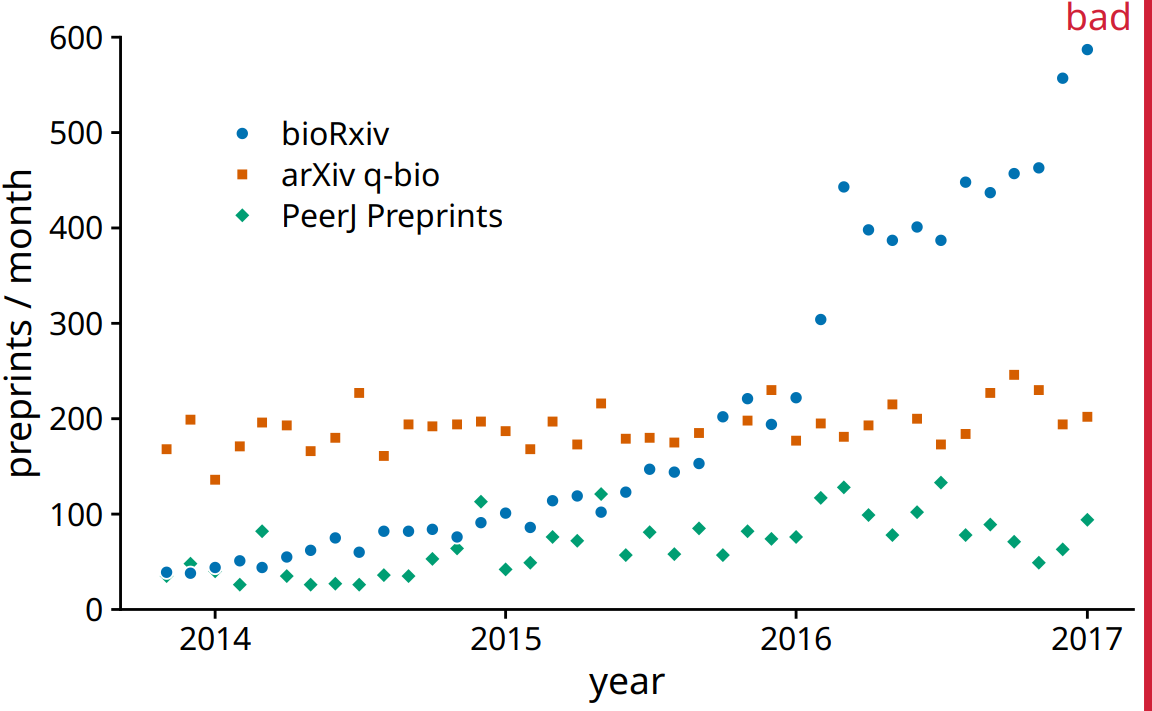
Figure 13.5: Monthly submissions to three preprint servers covering biomedical research: bioRxiv, the q-bio section of arXiv, and PeerJ Preprints. Each dot represents the number of submissions in one month to the respective preprint server. This figure is labeled “bad” because the three time courses visually interfere with each other and are difficult to read. Data source: Jordan Anaya, http://www.prepubmed.org/

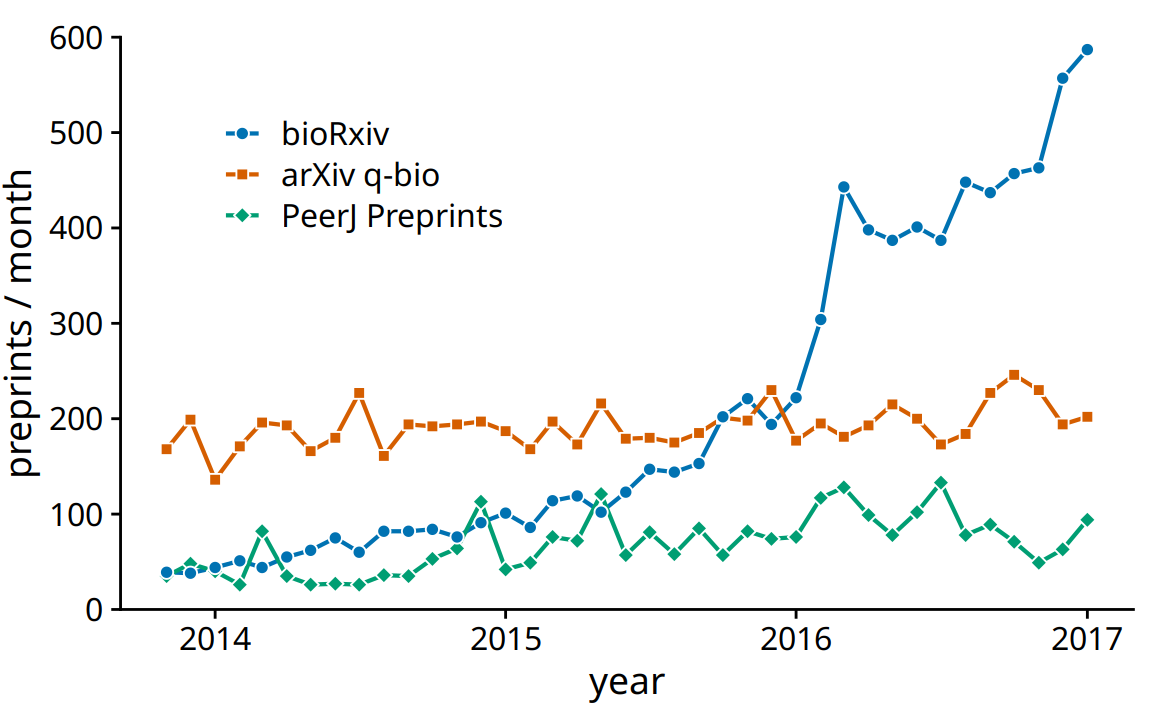
Figure 13.6: Monthly submissions to three preprint servers covering biomedical research. By connecting the dots in Figure 13.5 with lines, we help the viewer follow each individual time course. Data source: Jordan Anaya, http://www.prepubmed.org/

Figure 13.6 represents an acceptable visualization of the preprints dataset. However, the separate legend creates unnecessary cognitive load. We can reduce this cognitive load by labeling the lines directly (Figure 13.7). We have also eliminated the individual dots in this figure, for a result that is much more streamlined and easy to read than the original starting point, Figure 13.5.

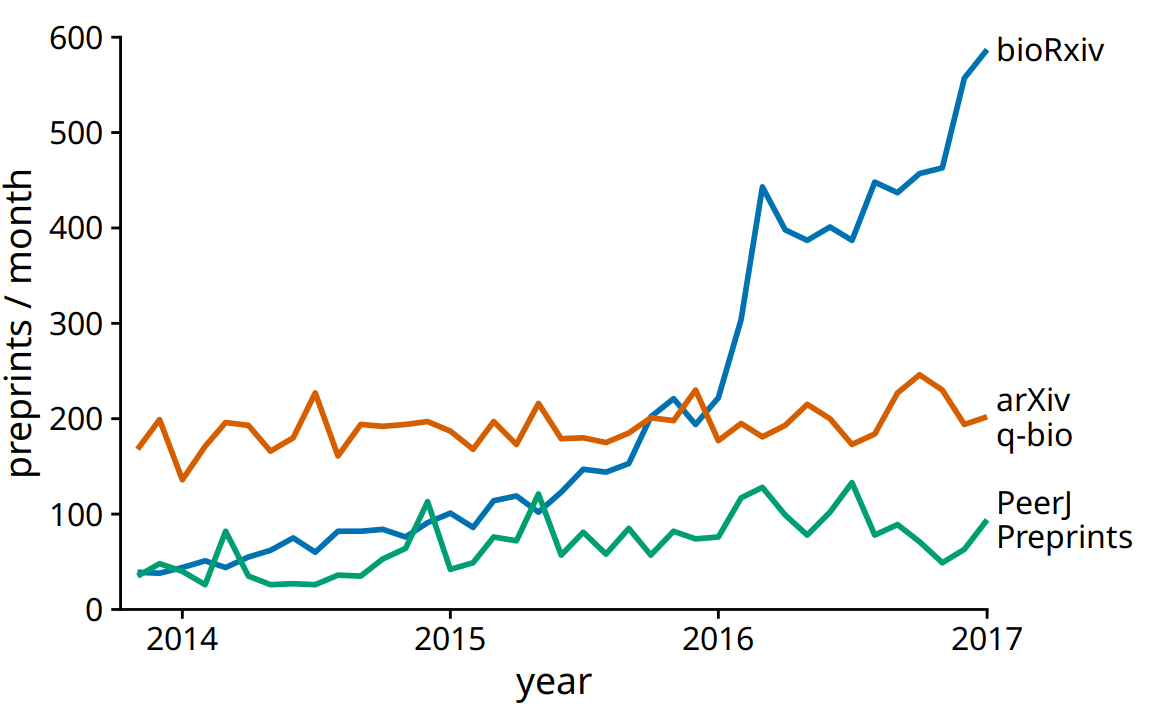
Figure 13.7: Monthly submissions to three preprint servers covering biomedical research. By direct labeling the lines instead of providing a legend, we have reduced the cognitive load required to read the figure. And the elimination of the legend removes the need for points of different shapes. Thus, we could streamline the figure further by eliminating the dots. Data source: Jordan Anaya, http://www.prepubmed.org/

Line graphs are not limited to time series. They are appropriate whenever the data points have a natural order that is reflected in the variable shown along the x axis, so that neighboring points can be connected with a line. This situation arises, for example, in dose–response curves, where we measure how changing some numerical parameter in an experiment (the dose) affects an outcome of interest (the response). Figure 13.8 shows a classic experiment of this type, measuring oat yield in response to increasing amounts of fertilization. The line-graph visualization highlights how the dose–response curve has a similar shape for the three oat varieties considered but differs in the starting point in the absence of fertilization (i.e., some varieties have naturally higher yield than others).

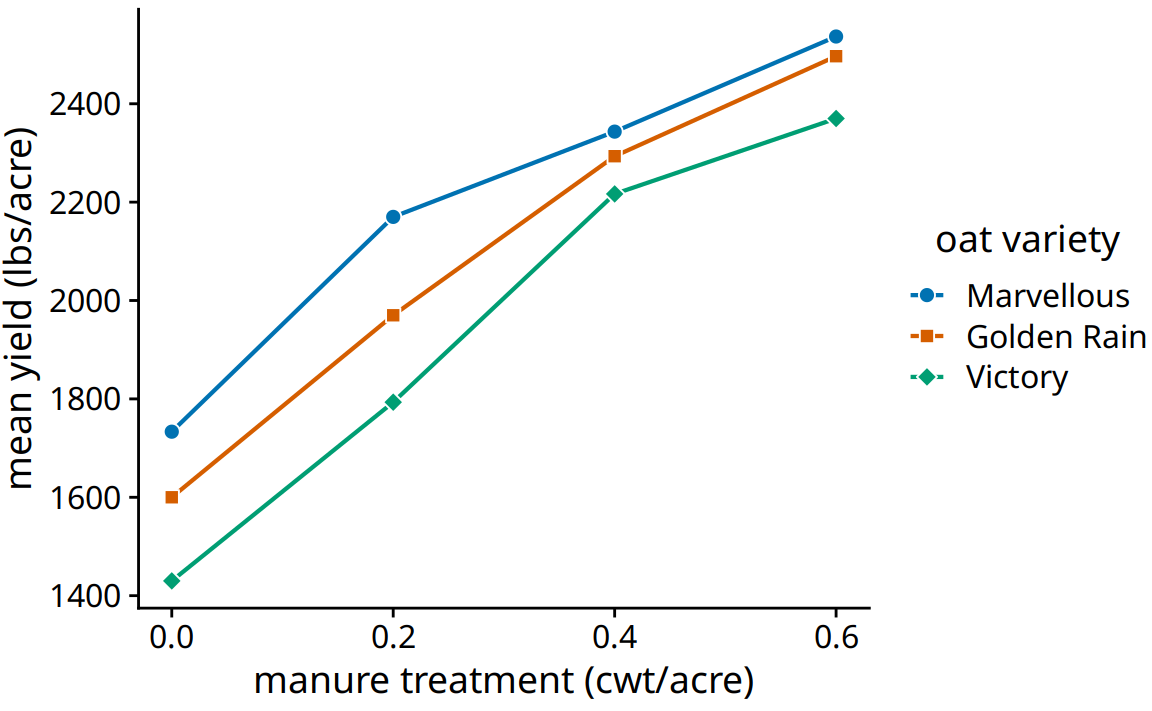
Figure 13.8: Dose–response curve showing the mean yield of oats varieties after fertilization with manure. The manure serves as a source of nitrogen, and oat yields generally increase as more nitrogen is available, regardless of variety. Here, manure application is measured in cwt (hundredweight) per acre. The hundredweight is an old imperial unit equal to 112 lbs or 50.8 kg. Data soure: Yates (1935)

13.3 Time series of two or more response variables

In the preceding examples we dealt with time courses of only a single response variable (e.g., preprint submissions per month or oat yield). It is not unusual, however, to have more than one response variable. Such situations arise commonly in macroeconomics. For example, we may be interested in the change in house prices from the previous 12 months as it relates to the unemployment rate. We may expect that house prices rise when the unemployment rate is low and vice versa.

Given the tools from the preceding subsections, we can visualize such data as two separate line graphs stacked on top of each other (Figure 13.9). This plot directly shows the two variables of interest, and it is straightforward to interpret. However, because the two variables are shown as separate line graphs, drawing comparisons between them can be cumbersome. If we want to identify temporal regions when both variables move in the same or in opposite directions, we need to switch back and forth between the two graphs and compare the relative slopes of the two curves.

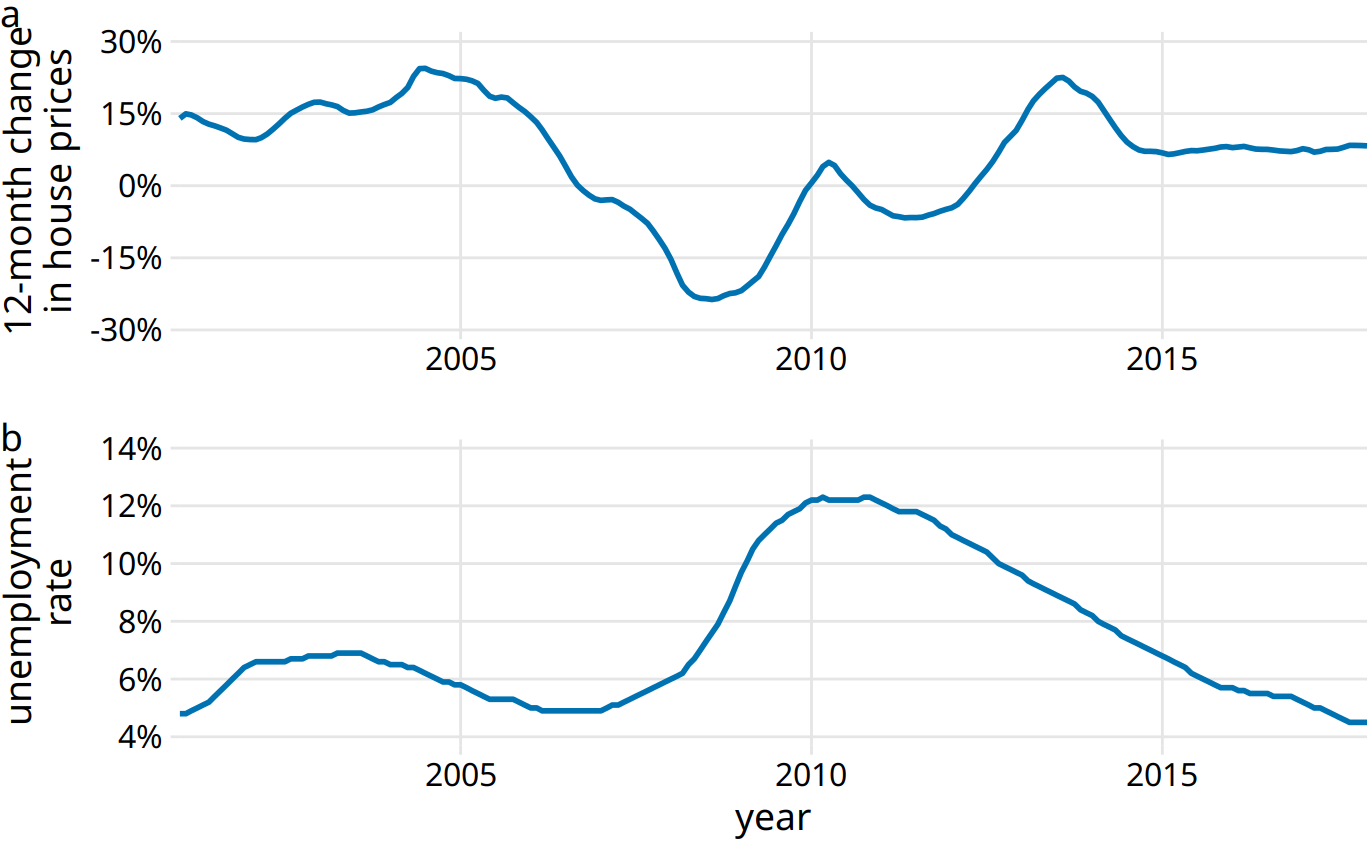
Figure 13.9: 12-month change in house prices (a) and unemployment rate (b) over time, from Jan. 2001 through Dec. 2017. Data sources: Freddie Mac House Prices Index, U.S. Bureau of Labor Statistics.

As an alternative to showing two separate line graphs, we can plot the two variables against each other, drawing a path that leads from the earliest time point to the latest (Figure 13.10). Such a visualization is called a connected scatter plot, because we are technically making a scatter plot of the two variables against each other and then are connecting neighboring points. Physicists and engineers often call this a phase portrait, because in their disciplines it is commonly used to represent movement in phase space. We have previously encountered connected scatter plots in Chapter 3, where we plotted the daily temperature normals in Houston, TX, versus those in San Diego, CA (Figure 3.3).

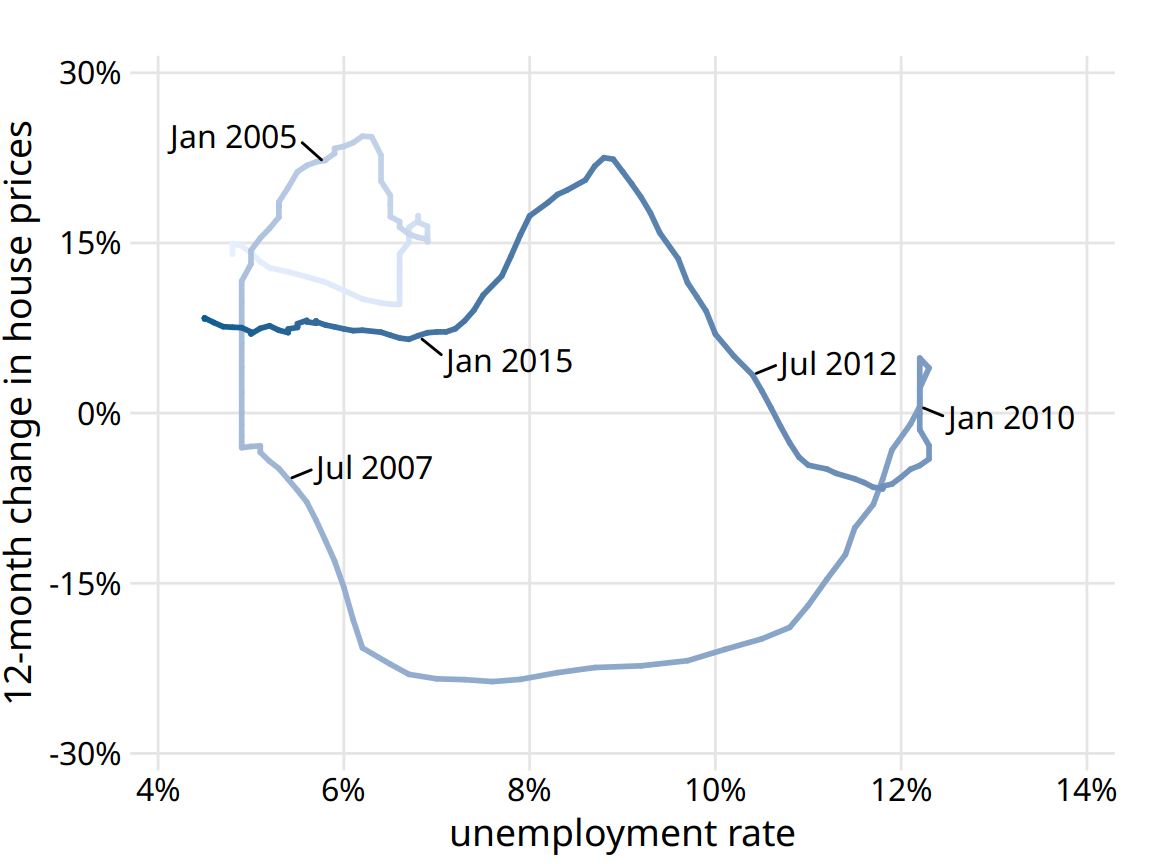
Figure 13.10: 12-month change in house prices versus unemployment rate, from Jan. 2001 through Dec. 2017, shown as a connected scatter plot. Darker shades represent more recent months. The anti-correlation seen in Figure 13.9 between the change in house prices and the unemployment rate causes the connected scatter plot to form two counter-clockwise circles. Data sources: Freddie Mac House Price Index, U.S. Bureau of Labor Statistics. Original figure concept: Len Kiefer

In a connected scatter plot, lines going in the direction from the lower left to the upper right represent correlated movement between the two variables (as one variable grows, so does the other), and lines going in the perpendicular direction, from the upper left to the lower right, represent anti-correlated movement (as one variable grows, the other shrinks). If the two variables have a somewhat cyclic relationship, we will see circles or spirals in the connected scatter plot. In Figure 13.10, we see one small circle from 2001 through 2005 and one large circle for the remainder of the time course.

When drawing a connected scatter plot, it is important that we indicate both the direction and the temporal scale of the data. Without such hints, the plot can turn into meaningless scribble (Figure 13.11). I am using here (in Figure 13.10) a gradual darkening of the color to indicate direction. Alternatively, one could draw arrows along the path.

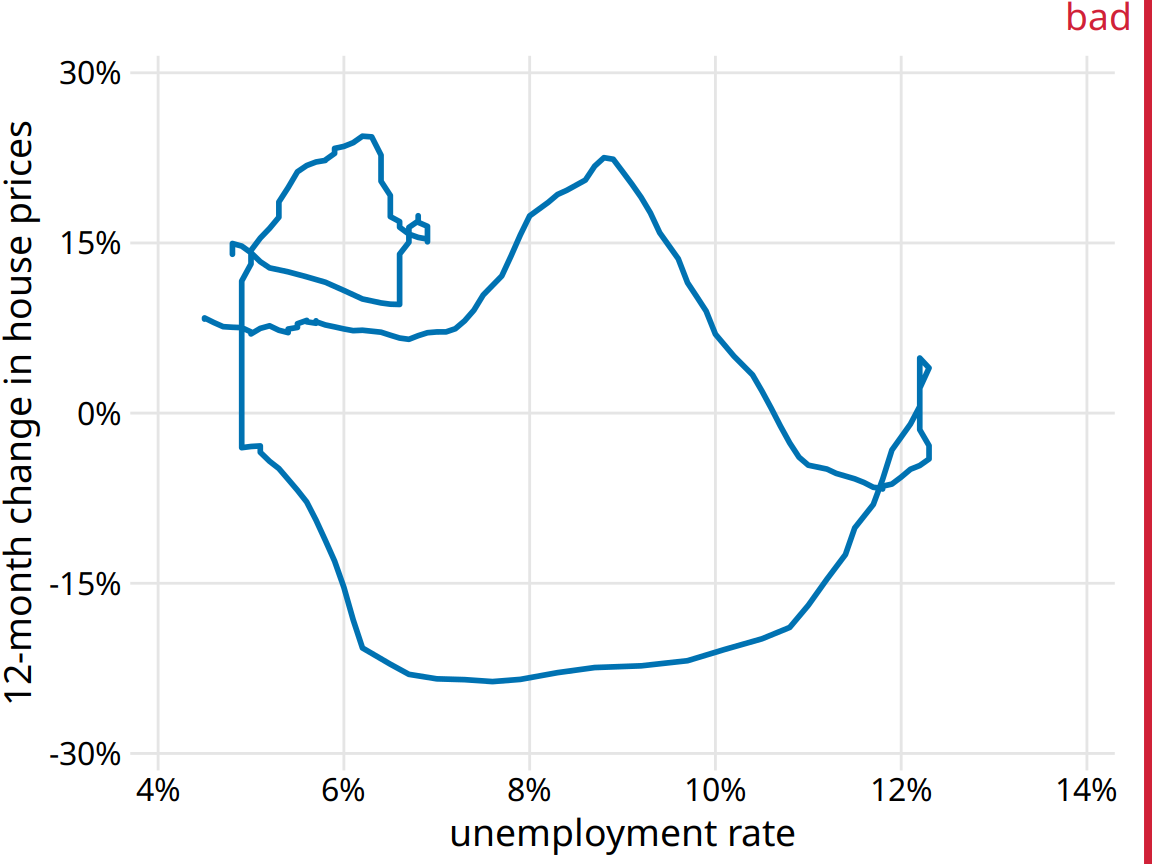
Figure 13.11: 12-month change in house prices versus unemployment rate, from Jan. 2001 through Dec. 2017. This figure is labeled “bad” because without the date markers and color shading of Figure 13.10, we can see neither the direction nor the speed of change in the data. Data sources: Freddie Mac House Prices Index, U.S. Bureau of Labor Statistics.

Is it better to use a connected scatter plot or two separate line graphs? Separate line graphs tend to be easier to read, but once people are used to connected scatter plots they may be able to extract certain patterns (such as cyclical behavior with some irregularity) that can be difficult to spot in line graphs. In fact, to me the cyclical relationship between change in house prices and unemployment rate is hard to spot in Figure 13.9, but the counter-clockwise spiral in Figure 13.10 clearly shows it. Research reports that readers are more likely to confuse order and direction in a connected scatter plot than in line graphs and less likely to report correlation (Haroz, Kosara, and Franconeri 2016). On the flip side, connected scatter plots seem to result in higher engagement, and thus such plots may be a effective tools to draw readers into a story (Haroz, Kosara, and Franconeri 2016).

Even though connected scatter plots can show only two variables at a time, we can also use them to visualize higher-dimensional datasets. The trick is to apply dimension reduction first (see Chapter 12). We can then draw a connected scatterplot in the dimension-reduced space. As an example of this approach, we will visualize a database of monthly observations of over 100 macroeconomic indicators, provided by the Federal Reserve Bank of St. Louis. We perform a principal components analysis (PCA) of all indicators and then draw a connected scatter plot of PC 2 versus PC 1 (Figure 13.12a) and versus PC 3 (Figure 13.12b).

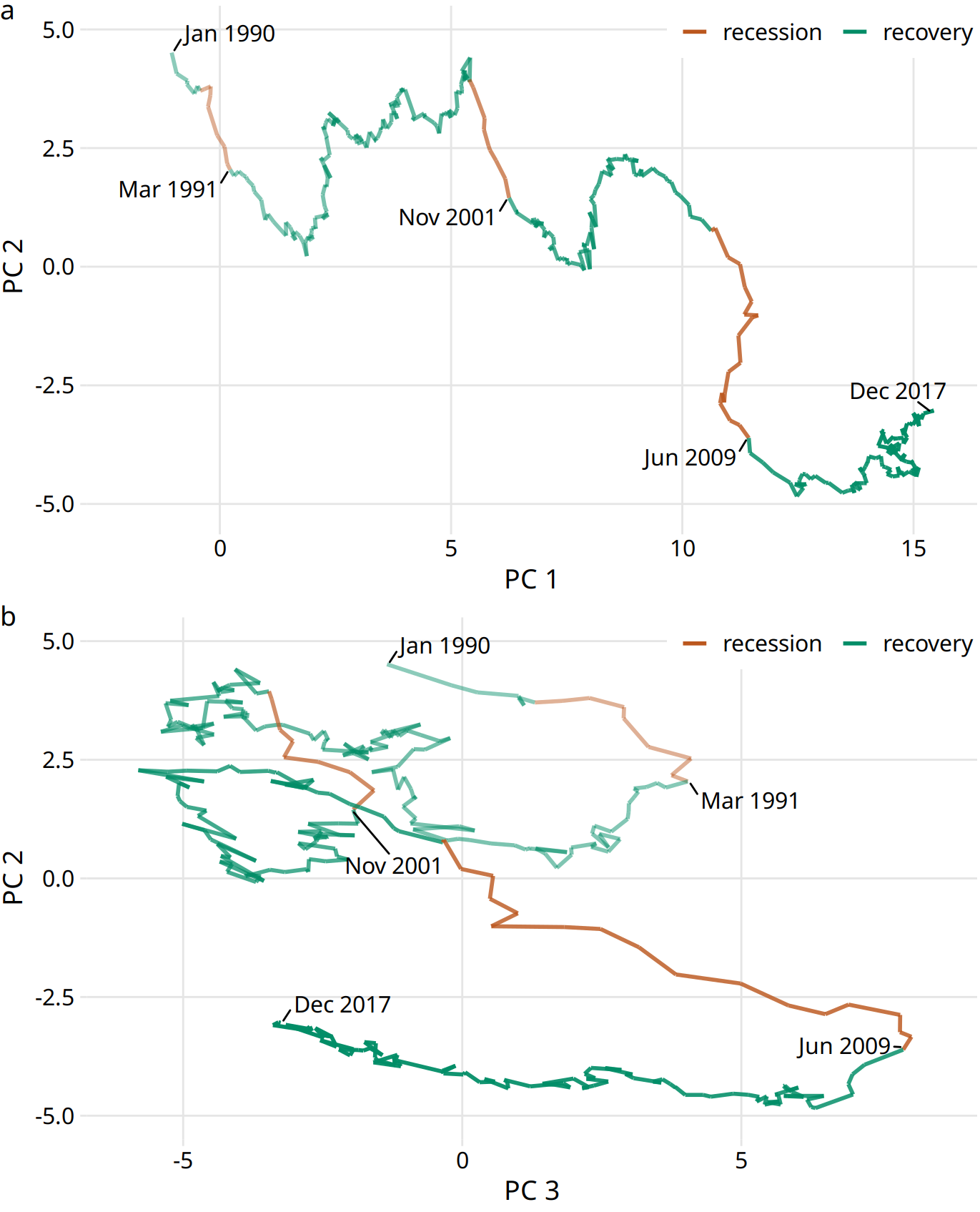
Figure 13.12: Visualizing a high-dimensional time series as a connected scatter plot in principal components space. The path indicates the joint movement of over 100 macroeconomic indicators from January 1990 to December 2017. Times of recession and recovery are indicated via color, and the end points of the three recessions (March 1991, November 2001, and June 2009) are also labeled. (a) PC 2 versus PC 1. (b) PC 2 versus PC 3. Data source: M. W. McCracken, St. Louis Fed

Notably, Figure 13.12a looks almost like a regular line plot, with time running from left to right. This pattern is caused by a common feature of PCA: The first component often measures the overall size of the system. Here, PC 1 approximately measures the overall size of the economy, which rarely decreases over time.

By coloring the connected scatter plot by times of recession and recovery, we can see that recessions are associated with a drop in PC 2 whereas recoveries do not correspond to a clear feature in either PC 1 or PC 2 (Figure 13.12a). The recoveries do, however, seem to correspond to a drop in PC 3 (Figure 13.12b). Moreover, in the PC 2 versus PC 3 plot, we see that the line follows the shape of a clockwise spiral. This pattern emphasizes the cyclical nature of the economy, with recessions following recoveries and vice versa.

References

Haroz, S., R. Kosara, and S. Franconeri. 2016. “The Connected Scatterplot for Presenting Paired Time Series.” IEEE Transactions on Visualization and Computer Graphics 22: 2174–86. https://doi.org/10.1109/TVCG.2015.2502587.

Yates, F. 1935. “Complex Experiments.” Supplement to the Journal of the Royal Statistical Society 2: 181–247. https://doi.org/10.2307/2983638.